练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设AB和CD是异面直线, M和N分别是线段AB和CD的中点, 比较MN与(BC+AD)的大小

    [　　]

    A.MN＞(BC+AD)　　B.MN＝ (BC+AD)

    C.MN＜(BC+AD)　　D.不确定

    答案：C
    解析：

    解: 连结BN并延长到E, 使NE＝ BN; 连结AE、DE.

    △ABE中, M是AB的中点, N是BE的中点, 所以AE＝ 2MN.

    又由∠DNE＝ ∠CNB,ND＝ CN, NE＝ BN, 得△DNE≌△CNB, 因而DE＝ BC. 

    现在证明D点不在线段AE上. 用反证法: 假使D点在AE上, 那么由于N点在BE上, 直线ND就在平面ABE上, 即AB与CD在同一平面内, 与已知矛盾. 所以D不在AE上, 由此得AE＜AD+DE, 即2MN＜AD+BC. 

    ∴MN＜(BC+AD)


    提示：

    		 连BN并延长到E, 使NE＝BN, 连AE, DE. 在△ADE中, 利用AE＜AD＋DE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    用反证法证明命题：“若直线AB、CD是异面直线，则直线AC、BD也是异面直线”的过程归纳为以下三个步骤：
    ①则A，B，C，D四点共面，所以AB、CD共面，这与AB、CD是异面直线矛盾；
    ②所以假设错误，即直线AC、BD也是异面直线；
    ③假设直线AC、BD是共面直线；
    则正确的序号顺序为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

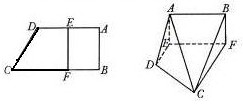    （2010•湖北模拟）如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，当E、F分别在线段AD、BC上，且EF⊥BC，AD=3，BC=4，AE=2，现将梯形ABCD沿EF折叠，使平面ABFE与平面EFCD垂直．
    （1）证明：直线AB与CD是异面直线；
    （2）当直线AC与平面EFCD所成角为30°时，求二面角A-DC-E的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

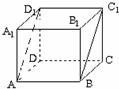    精英家教网如图，ABCD-A1B1C1D1为正方体，下面结论错误的是（　　）
    A、AD∥平面CB1D1B、AC1⊥BDC、AC1⊥平面CB1D1D、AD1和CD是异面直线

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    已知A、B、C、D是空间四点, 并且AB和CD是异面直线, 那么AD和BC是两条_________

    查看答案和解析>>

    同步练习册答案