
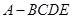 中,平面
中,平面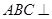 平面
平面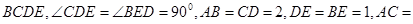
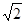 .
.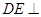 平面
平面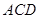 ;
;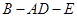 的大小
的大小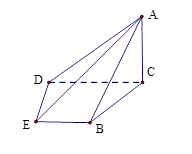
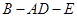 的大小是
的大小是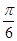 .
.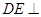 平面
平面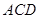 ,证明线面垂直,先证线线垂直,即证线和平面内两条相交直线垂直,由已知可得
,证明线面垂直,先证线线垂直,即证线和平面内两条相交直线垂直,由已知可得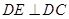 ,只需证明
,只需证明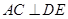 ,或
,或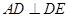 ,由已知平面
,由已知平面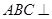 平面
平面 ,只需证明
,只需证明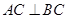 ,就得
,就得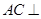 平面
平面 ,即
,即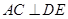 ,而由已知
,而由已知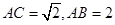 ,在直角梯形
,在直角梯形 中,易求
中,易求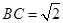 ,从而满足
,从而满足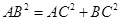 ,即得
,即得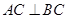 ,问题得证;(2)求二面角
,问题得证;(2)求二面角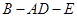 的大小,可用传统方法,也可用向量法,用传统方法,关键是找二面角的平面角,可利用三垂线定理来找,但本题不存在利用三垂线定理的条件,因此利用垂面法,即作
的大小,可用传统方法,也可用向量法,用传统方法,关键是找二面角的平面角,可利用三垂线定理来找,但本题不存在利用三垂线定理的条件,因此利用垂面法,即作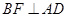 ,与
,与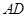 交于点
交于点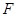 ,过点
,过点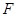 作
作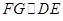 ,与
,与 交于点
交于点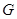 ,连结
,连结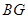 ,由(1)知,
,由(1)知,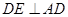 ,则
,则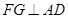 ,,所以
,,所以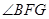 是二面角
是二面角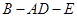 的平面角,求出
的平面角,求出 的三条边,利用余弦定理,即可求出二面角
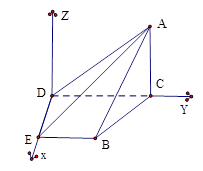
的三条边,利用余弦定理,即可求出二面角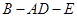 的大小,用向量法,首先建立空间坐标系,先找三条两两垂直的直线作为坐标轴,观察几何图形可知,以
的大小,用向量法,首先建立空间坐标系,先找三条两两垂直的直线作为坐标轴,观察几何图形可知,以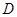 为原点,分别以射线
为原点,分别以射线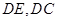 为
为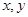 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系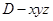 ,写出个点坐标,设出设平面
,写出个点坐标,设出设平面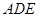 的法向量为
的法向量为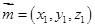 ,平面
,平面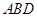 的法向量为
的法向量为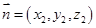 ,求出它们的一个法向量,利用法向量的夹角与二面角的关系,即可求出二面角
,求出它们的一个法向量,利用法向量的夹角与二面角的关系,即可求出二面角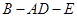 的大小.
的大小. 中,由
中,由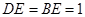 ,
,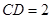 得,
得,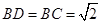 ,由
,由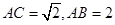 ,则
,则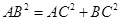 ,即
,即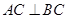 ,又平面
,又平面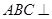 平面
平面 ,从而
,从而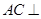 平面
平面 ,所以
,所以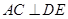 ,又
,又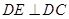 ,从而
,从而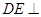 平面
平面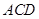 ;
;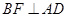 ,与
,与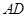 交于点
交于点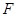 ,过点
,过点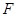 作
作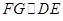 ,与
,与 交于点
交于点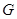 ,连结
,连结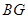 ,由(1)知,
,由(1)知,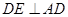 ,则
,则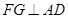 ,,所以
,,所以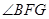 是二面角
是二面角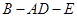 的平面角,在直角梯形
的平面角,在直角梯形 中,由
中,由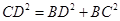 ,得
,得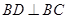 ,又平面
,又平面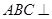 平面
平面 ,得
,得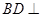 平面
平面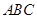 ,从而,
,从而,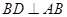 ,由于
,由于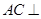 平面
平面 ,得:
,得: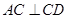 ,在
,在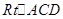 中,由
中,由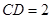 ,
,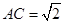 ,得
,得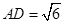 ,
,
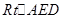 中,
中,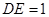 ,
,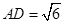 ,得
,得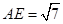 ,在
,在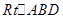 中,
中,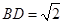 ,
,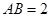 ,
,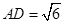 ,得
,得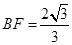 ,
,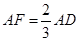 ,从而
,从而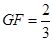 ,在
,在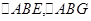 中,利用余弦定理分别可得
中,利用余弦定理分别可得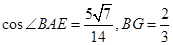 ,在
,在 中,
中,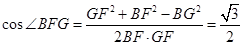 ,所以
,所以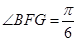 ,即二面角
,即二面角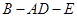 的大小是
的大小是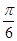 .
.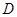 为原点,分别以射线
为原点,分别以射线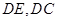 为
为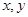 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系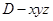 如图所示,由题意可知各点坐标如下:
如图所示,由题意可知各点坐标如下: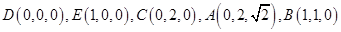 ,设平面
,设平面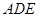 的法向量为
的法向量为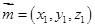 ,平面
,平面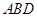 的法向量为
的法向量为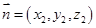 ,可算得
,可算得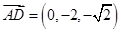 ,
,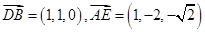 ,由
,由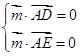 得,
得,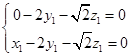 ,可取
,可取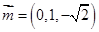 ,由
,由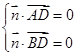 得,
得,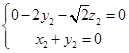 ,可取
,可取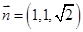 ,于是
,于是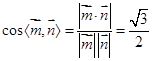 ,由题意可知,所求二面角是锐角,故二面角
,由题意可知,所求二面角是锐角,故二面角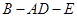 的大小是
的大小是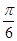 .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源:不详 题型:解答题
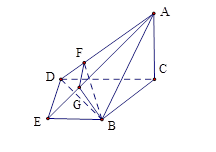
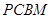 是直角梯形,∠
是直角梯形,∠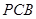 =90°,
=90°,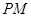 ∥
∥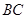 ,
,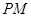 =1,
=1,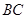 =2,又
=2,又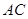 =1,∠
=1,∠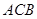 =120°,
=120°,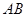 ⊥
⊥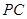 ,直线
,直线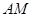 与直线
与直线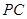 所成的角为60°.
所成的角为60°.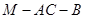 的的余弦值;
的的余弦值; 到面
到面 的距离.
的距离.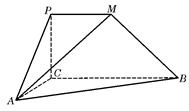
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
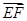 ·
·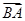 ;
;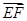 ·
·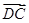 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
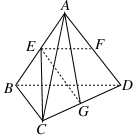
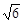 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记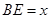 ,用
,用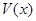 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.
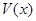 的表达式;
的表达式;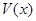 取得最大值?
取得最大值?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
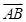 ,
,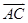 为边的平行四边形的面积;
为边的平行四边形的面积;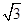 ,且a分别与
,且a分别与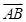 ,
,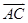 垂直,求向量a的坐标.
垂直,求向量a的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com