
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
【答案】(1)an=3n﹣1;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)设出数列的公差,分别根据等差数列的通项公式表示出![]() 和
和![]() 联立方程求得和
联立方程求得和![]() 和
和![]() ,则数列的通项公式可得,求出首项与公比,即可得
,则数列的通项公式可得,求出首项与公比,即可得![]() 的通项公式;(2)由(1)得的
的通项公式;(2)由(1)得的![]() 代入
代入![]() ,利用错位相减求和即可.
,利用错位相减求和即可.
试题解析:(1)设公差为d,则由a2=5,S5=40,得:![]() ,解得
,解得![]() ,则an=3n﹣1…
,则an=3n﹣1…
∵![]() ∴q=3
∴q=3![]() …
…
(2)![]() ①
①
∴![]() ②
②
①﹣②:![]()
∴![]() …
…
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列,![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”
”![]() 与“
与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,侧面
,侧面![]() 是边长为2的等边三角形,点
是边长为2的等边三角形,点![]() 是
是![]() 的中点,且平面
的中点,且平面![]() 平面
平面![]() .
.
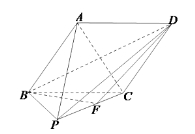
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)若点![]() 在线段
在线段![]() 上移动,是否存在点
上移动,是否存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,指出点
?若存在,指出点![]() 的位置,否则说明理由.
的位置,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据俄罗斯新罗西斯克2015年5月17日电 记者吴敏、郑文达报道:当地时间17日,参加中俄“海上联合-2015(Ⅰ)”军事演习的9艘舰艇抵达地中海预定海域,混编组成海上联合集群.接到命令后我军在港口M要将一件重要物品用小艇送到一艘正在航行的俄军轮船上,在小艇出发时,轮船位于港口M北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值并说明你的推理过程;
(3)是否存在v,使得小艇以v海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X~N(μ,σ2),且其正态曲线在(-∞,80)上是增函数,在(80,+∞)上为减函数,且P(72≤X≤88)=0.682 6.
(1)求参数μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
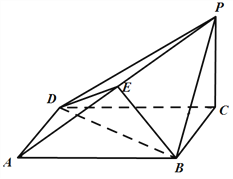
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,点
为正方形,点![]() 是棱
是棱![]() 的中点,
的中点,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求证:![]() //平面
//平面![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ) 设![]() ,试判断平面
,试判断平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,写出
能否成立;若成立,写出![]() 的一个值(只需写出结论).
的一个值(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com