
【题目】如图,矩形ABCD中,![]() ,
,![]() ,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将
,E,F分别为AD,AB中点,M为线段BC上的一个动点,现将![]() ,
,![]() ,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为
,分别沿EC,EF折起,使A,D重合于点P.设PM与平面BCEF所成角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,二面角
,二面角![]() 的平面角为
的平面角为![]() ,则( )
,则( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
过![]() 作
作![]()
![]() 平面
平面![]() ,作出三个二面角
,作出三个二面角![]() ,二面角
,二面角![]() 的平面角,二面角
的平面角,二面角![]() 的平面角,通过原平面图形计算可得这三个角的大小关系.从而得出结论.
的平面角,通过原平面图形计算可得这三个角的大小关系.从而得出结论.
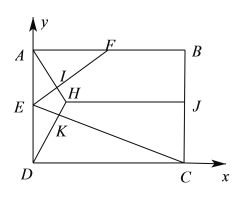
在![]() 翻折过程中,A点在底面的投影在过点A且垂直EF的直线上(设垂足为I),同理在
翻折过程中,A点在底面的投影在过点A且垂直EF的直线上(设垂足为I),同理在![]() 翻折过程中,D点在底面的投影在过点D且垂直EC的直线上(设垂足为K),设点P在底面的投影为点H,过点H向BC作垂线HJ(垂足为J),
翻折过程中,D点在底面的投影在过点D且垂直EC的直线上(设垂足为K),设点P在底面的投影为点H,过点H向BC作垂线HJ(垂足为J),
把![]() ,
,![]() 摊平到原来的平面图形,如下右图,
摊平到原来的平面图形,如下右图,![]() 就是
就是![]() 和
和![]() 延长线的交点,由已知可得
延长线的交点,由已知可得![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,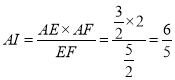 ,同理可得
,同理可得![]() ,
,![]() ,则在左图中知易得
,则在左图中知易得![]() ,由二面角的定义知
,由二面角的定义知![]() ,所以
,所以![]() ,
,
又在右图中,以![]() ,
,![]() 为
为![]() 轴建立平面直角坐标系,
轴建立平面直角坐标系,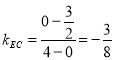 ,则
,则![]() ,直线
,直线![]() 方程为
方程为![]() ,同理直线
,同理直线![]() 的方程为
的方程为![]() ,由
,由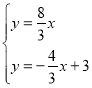 得
得![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]() ,所以二面角
,所以二面角![]() 的平面角小于二面角
的平面角小于二面角![]() 的平面角,显然
的平面角,显然![]() 不大于二面角
不大于二面角![]() 的平面角,∴
的平面角,∴![]() ,综上可知
,综上可知![]() ,
,
故选:D



科目:高中数学 来源: 题型:
【题目】2020年1月,某公司以问卷的形式调查影响员工积极性的六项关键指标:绩效奖励、排班制度、激励措施、工作环境、人际关系、晋升渠道,在确定各项指标权重结果后,进而得到指标重要性分析象限图(如图).若客户服务中心从中任意抽取不同的两项进行分析,则这两项来自影响稍弱区的概率为( )
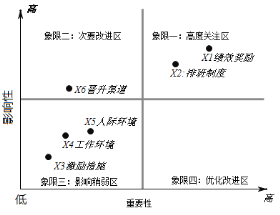
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(2)设点过![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且满足
上的点,且满足![]() 为等边三角形,求
为等边三角形,求![]() 边长的取值范围.
边长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,又函数![]() .
.
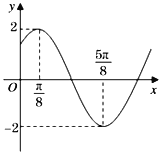
(1)求函数![]() 的单调减区间;
的单调减区间;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,又![]() ,且锐角C满足
,且锐角C满足![]() ,若sinB=2sinA,求a+b的值.
,若sinB=2sinA,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(Ⅱ)若该市政府拟采取分层抽样的方法在用水量吨数为![]() 和
和![]() 之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设
之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖的家庭数,
中的获奖的家庭数,![]() 为用水量吨数在
为用水量吨数在![]() 中的获奖家庭数,记随机变量
中的获奖家庭数,记随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较甲,乙两地某月![]() 时的气温,随机选取该月中的
时的气温,随机选取该月中的![]() 天,将这
天,将这![]() 天中
天中![]() 时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月
时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:①甲地该月![]() 时的平均气温低于乙地该月
时的平均气温低于乙地该月![]() 时的平均气温;②甲地该月
时的平均气温;②甲地该月![]() 时的平均气温高于乙地该月
时的平均气温高于乙地该月![]() 时的平均气温;③甲地该月
时的平均气温;③甲地该月![]() 时的气温的中位数小于乙地该月
时的气温的中位数小于乙地该月![]() 时的气温的中位数;④甲地该月
时的气温的中位数;④甲地该月![]() 时的气温的中位数大于乙地该月
时的气温的中位数大于乙地该月![]() 时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )
时的气温的中位数.其中根据茎叶图能得到的正确结论的编号为( )

A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某中学理学社为了吸收更多新社员,在校团委的支持下,在高一学年组织了抽签赠书活动.月初报名,月末抽签,最初有30名同学参加.社团活动积极分子甲同学参加了活动.
①第一个月有18个中签名额.甲先抽签,乙和丙紧随其后抽签.求这三名同学同时中签的概率.
②理学社设置了第![]() (
(![]() )个月中签的名额为
)个月中签的名额为![]() ,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
,并且抽中的同学退出活动,同时补充新同学,补充的同学比中签的同学少2个,如果某次抽签的同学全部中签,则活动立刻结束.求甲同学参加活动时间的期望.
(2)某出版集团为了扩大影响,在全国组织了抽签赠书活动.报名和抽签时间与(1)中某中学理学社的报名和抽签时间相同,最初有30万人参加,甲同学在其中.每个月抽中的人退出活动,同时补充新人,补充的人数与中签的人数相同.出版集团设置了第![]() (
(![]() )个月中签的概率为
)个月中签的概率为![]() ,活动进行了
,活动进行了![]() 个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于
个月,甲同学很幸运,中签了,在此条件下,求证:甲同学参加活动时间的均值小于![]() 个月.
个月.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com