
�������У�1������2������3������ѡ���⣬ÿ��7�֣��뿼����ѡ2����������14�֣������������������ǰ����Ƿ֣�����ʱ������2BǦ���ڴ���ϰ���ѡ��Ŀ��Ӧ�����Ϳ�ڣ�������ѡ������������У�
(1)��ѡ��4��2 ������任������С������7�֣�
��֪����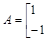
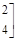 ������
������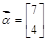 ��
��
(��)
�����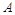 ������ֵ
������ֵ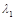 ��
��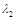 ����������
����������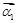 ��
��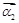 ��
��
������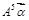 ��ֵ��
��ֵ��
(2)��ѡ��4��4 ���������뼫���꣩����С������7�֣�
�ڼ�����ϵ��,������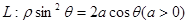 ���һ��
���һ��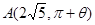 (����
(����
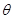 Ϊ���)��ƽ����
Ϊ���)��ƽ����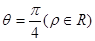 ��ֱ��
��ֱ��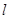 �����߷ֱ���
�����߷ֱ��� ��
��
(��)
д������ ��ֱ��
��ֱ��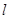 ����ͨ����(�Լ���Ϊԭ��,����Ϊ
����ͨ����(�Լ���Ϊԭ��,����Ϊ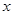 ��������Ὠϵ)��
��������Ὠϵ)��
������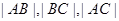 �ɵȱ�����,��
�ɵȱ�����,��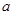 ��ֵ��
��ֵ��
(3)��ѡ��4��5 ����ʽ֤��ѡ��������С������7�֣�
��֪��ʵ�� ��
�� ��
��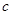 ��������
��������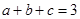 ��
��
(��)
��֤��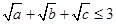 ��
��
������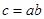 ����
����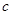 �����ֵ��
�����ֵ��
�ž�����任
�⣺(��)����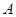 ����������ʽΪ
����������ʽΪ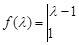
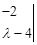
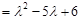 ��
��
��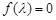 ����
����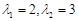 ,
,
��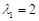 ʱ����
ʱ����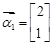 ,��
,��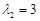 ʱ����
ʱ����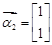 . ������������������3��
. ������������������3��
������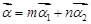 ��
�� ����
����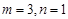 .
.
��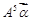
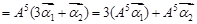
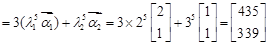 .������������������7��
.������������������7��
�Ʋ��������뼫����
�⣺(��)  ������������������3��
������������������3��
����ֱ��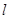 �IJ�������Ϊ
�IJ�������Ϊ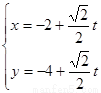 (
(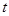 ����),����
Ϊ����),����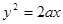 �õ�
�õ�
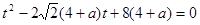 ,����
,����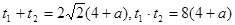
��Ϊ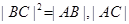 ,����
,����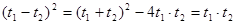
��� 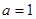 ������������������7��
������������������7��
�Dz���ʽ֤��ѡ��
�⣺(��)�ɿ�������ʽ��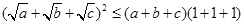
������֪ a+b+c=3
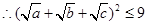
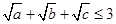
���ҽ��� a=b=c=1��ȡ�Ⱥš�������������������3��
������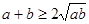 ��
��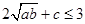 ����
����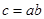 ����
����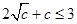 ��
��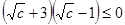 ��
��
����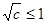 ��
��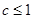 �����ҽ��� a=b= 1ʱ��
�����ҽ��� a=b= 1ʱ��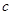 �����ֵ1��������������������7��
�����ֵ1��������������������7��
����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
| 2 |
| �� |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
|
| 12 |
| 3cos2��+4sin2�� |
|
| x |
| yz |
| y |
| zx |
| z |
| xy |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
| 7 |
| 4 |
| x2 |
| 16 |
| y2 |
| 5 |
| z2 |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
|
a2+
|
| 2 |
| 1 |
| a |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com