
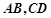 的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9
的底部都在同一个水平面上,且均与水平面垂直,它们的高度分别是9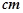 和15
和15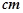 ,从建筑物
,从建筑物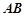 的顶部
的顶部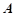 看建筑物
看建筑物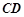 的视角
的视角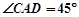 .
.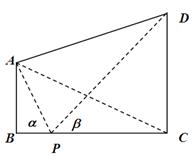
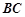 的长度;
的长度;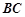 上取一点
上取一点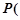 点
点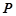 与点
与点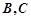 不重合),从点
不重合),从点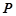 看这两座建筑物的视角分别为
看这两座建筑物的视角分别为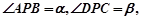 问点
问点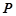 在何处时,
在何处时,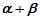 最小?
最小?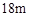 ;⑵当
;⑵当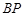 为
为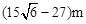 时,
时,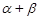 取得最小值.
取得最小值.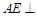
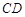 ,垂足为
,垂足为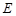 ,则可题中所有条件集中到两个直角三角形
,则可题中所有条件集中到两个直角三角形 中,由
中,由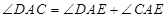 ,而在
,而在 中
中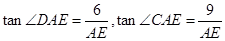 ,再由两角和的正切公式即可求出
,再由两角和的正切公式即可求出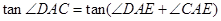 的值,又
的值,又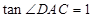 ,可求出
,可求出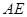 的值;⑵由题意易得在两直角三角形
的值;⑵由题意易得在两直角三角形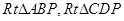 中,可得
中,可得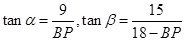 ,再由两角和的正切公式可求出
,再由两角和的正切公式可求出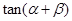 的表达式,由函数
的表达式,由函数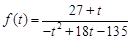 的特征,可通过导数求出函数的单调性和最值,进而求出
的特征,可通过导数求出函数的单调性和最值,进而求出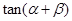 的最小值,即可确定出
的最小值,即可确定出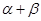 的最小值.
的最小值.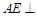
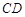 ,垂足为
,垂足为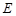 ,则
,则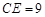 ,
,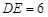 ,设
,设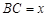 ,
,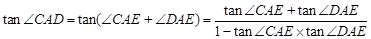 2分
2分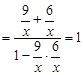 ,化简得
,化简得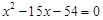 ,解之得,
,解之得,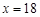 或
或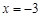 (舍)
(舍) 的长度为
的长度为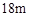 . 6分
. 6分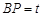 ,则
,则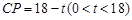 ,
,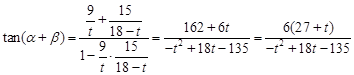 . 8分
. 8分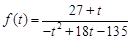 ,
,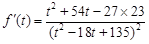 ,令
,令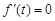 ,因为
,因为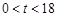 ,得
,得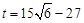 ,当
,当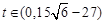 时,
时,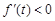 ,
,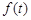 是减函数;当
是减函数;当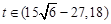 时,
时,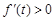 ,
,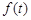 是增函数,
是增函数,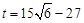 时,
时,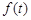 取得最小值,即
取得最小值,即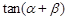 取得最小值, 12分
取得最小值, 12分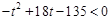 恒成立,所以
恒成立,所以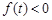 ,所以
,所以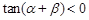 ,
, ,
,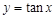 在
在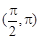 上是增函数,所以当
上是增函数,所以当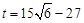 时,
时,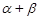 取得最小值.
取得最小值.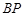 为
为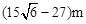 时,
时,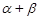 取得最小值. 14分
取得最小值. 14分

科目:高中数学 来源:不详 题型:解答题
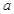
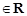 ).
).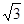 cosx)(
cosx)(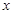
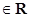 )的最大值为
)的最大值为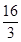 ,求f(x)的最小值;
,求f(x)的最小值;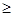 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp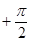 (k∈Z).
(k∈Z).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com