
记有限集合A的元素个数为n(A),那么有n(A∪B)=n(A)+n(B)-n(A∩B);n(A∪B∪C)=n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C).解下列题目:一次会议有1990位数学家参加,每人至少有1327位合作者,求证:可以找到千位数学家,他们中每两个人都合作过.
|
解:记数学家们为Vi(i=1,2,3,…,1990),与Vi合作过的数学家组成集合Ai,任取合作过的两位数学家记为V1,V2,则n(A1)≥1327,n(A1)≥1327,n(A1∪A2)≤1990,得n(A1∩A2)=n(A1)+n(A2)-n(A1∪A2)≥1327×2-1990>0,从而存在数学家V3∈A1∩A2,V3≠V1,V3≠V2 又∵n(A1∩A2∩A3)=n(A1∩A2)+n(A3)-n[(A1∩A2)∪A3]≥[(1327×2)-1990]+1327-1990=1 ∴存在数学家V4∈A1∩A2∩A3,V4≠V1,V4≠V2,V4≠V3 ∴数学家V1,V2,V3,V4两两合作过. 从而问题得证. 思想方法小结:本题实质是证明A1∩A2∩A3≠φ. |
|
将实际问题,转化为数学问题,利用集合思想加以解决,充分利用上面两个集合元素个数的公式. |


科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| k |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
有限集合A的元素个数记作card(A).如A={a,b,c,d},则card(A)=4.一般地,对于任意两个集合A、B,有:
card(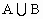 )=card(A)+card(B)-card(
)=card(A)+card(B)-card(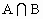 ).
).
两个变形公式为:
card(A)+card(B)=card(A∪B)+card(A∩B);
card(A∩B)=card(A)+card(B)-card(A∪B).
请根据以上知识解下题.
学校举办了一次田径运动会,某班有8名同学参赛,又举办了一次球类运动会,这个班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有多少名同学参赛?
查看答案和解析>>
科目:高中数学 来源: 题型:044
有限集合
A的元素个数记作card(A).如A={a,b,c,d},则card(A)=4.一般地,对于任意两个集合A、B,有:card(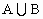 )=card(A)
)=card(A)
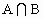 ).
).
两个变形公式为:
card(A)
+card(B)=card(A∪B)+card(A∩B);card(A
∩B)=card(A)+card(B)-card(A∪B).请根据以上知识解下题.
学校举办了一次田径运动会,某班有
8名同学参赛,又举办了一次球类运动会,这个班有12名同学参赛,两次运动会都参赛的有3人.两次运动会中,这个班共有多少名同学参赛?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com