
【题目】若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)-log3|x|的零点个数是( )
A.多于4个
B.4个
C.3个
D.2个
【答案】B
【解析】若函数f(x)满足f(x+2)=f(x),
则函数是以2为周期的周期函数,
又由函数是定义在R上的偶函数,
结合当x∈[0,1]时,f(x)=x,
我们可以在同一坐标系中画出函数y=f(x)与函数y=log3|x|的图象如下图所示: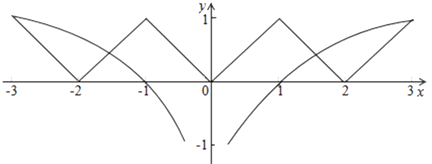
由图可知函数y=f(x)与函数y=log3|x|的图象共有4个交点,
即函数y=f(x)﹣log3|x|的零点个数是4个,
所以答案是:B.
【考点精析】本题主要考查了函数的零点与方程根的关系和函数的零点的相关知识点,需要掌握二次函数的零点:(1)△>0,方程 有两不等实根,二次函数的图象与 轴有两个交点,二次函数有两个零点;(2)△=0,方程 有两相等实根(二重根),二次函数的图象与 轴有一个交点,二次函数有一个二重零点或二阶零点;(3)△<0,方程 无实根,二次函数的图象与 轴无交点,二次函数无零点;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能正确解答此题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=a(x﹣1)2﹣xe2﹣x .
(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线与x轴平行,求a的值;
(Ⅱ)若 ![]() ,求f(x)的单调区间.
,求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在以
为参数),在以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 ![]() 是圆心为
是圆心为 ![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线 ![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 为曲线
为曲线 ![]() 上的点,
上的点, ![]() 为曲线
为曲线 ![]() 上的点,求
上的点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.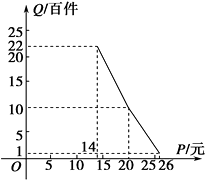
(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是偶函数,当x>0时,f(x)单调递减,设a=-21.2 , ![]() ,c=2log52,则f(a),f(b),f(c)的大小关系为( )
,c=2log52,则f(a),f(b),f(c)的大小关系为( )
A.f(c)<f(b)<f(a)
B.f(c)<f(a)<f(b)
C.f(c)>f(b)>f(a)
D.f(c)>f(a)>f(b)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com