解:(Ⅰ)f(x)的定义域为R,且 f'(x)=e
x+a.
①当a=0时,f(x)=e
x,故f(x)在R上单调递增.
从而f(x)没有极大值,也没有极小值.
②当a<0时,令f'(x)=0,得x=ln(-a).f(x)和f'(x)的情况如下:
| x | (-∞,ln(-a)) | ln(-a) | (ln(-a),+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | | ↗ |
故f(x)的单调减区间为(-∞,ln(-a));单调增区间为(ln(-a),+∞).
从而f(x)的极小值为f(ln(-a))=-a+aln(-a);没有极大值.
(Ⅱ)g(x)的定义域为(0,+∞),且
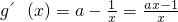
.
③当a=0时,f(x)在R上单调递增,g(x)在(0,+∞)上单调递减,不合题意.
④当a<0时,g'(x)<0,g(x)在(0,+∞)上单调递减.
当-1≤a<0时,ln(-a)≤0,此时f(x)在(ln(-a),+∞)上单调递增,由于g(x)在(0,+∞)上单调递减,不合题意.
当a<-1时,ln(-a)>0,此时f(x)在(-∞,ln(-a))上单调递减,由于f(x)在(0,+∞)上单调递减,符合题意.
综上,a的取值范围是(-∞,-1).
分析:(I)由导数运算法则知,f'(x)=e
x+a,对字母a进行分类讨论,再利用导数与单调性关系求出极值即可;
(II)对于存在性问题,可先假设存在,即假设存在实数a的值,使函数f(x)和函数g(x)在M上具有相同的单调性,再利用导数工具,求出函数的单调区间,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本题主要考查利用导数研究函数的单调性,考查函数、导数、不等式等基础知识,以及综合运用上述知识分析问题和解决问题的能力.

 .
.
