
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的离心率
(a>b>0)的离心率 ![]() ,且点
,且点 ![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的方程;
(Ⅱ)直线l与椭圆E交于A、B两点,且线段AB的垂直平分线经过点 ![]() .求△AOB(O为坐标原点)面积的最大值.
.求△AOB(O为坐标原点)面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点M到点
中,点M到点![]() 的距离比它到
的距离比它到![]() 轴的距离大2,记点M的轨迹为C.
轴的距离大2,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)若直线![]() 与轨迹C恰有2个公共点,求实数b的取值范围.
与轨迹C恰有2个公共点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数g(x)满足g(g(x))=n(n∈N)有n+3个解,则称函数g(x)为“复合n+3解”函数.已知函数f(x)= 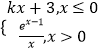 (其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
(其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
A.(﹣∞,0)
B.(﹣e,e)
C.(﹣1,1)
D.(0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,倾斜角为α(α≠ ![]() )的直线l的参数方程为
)的直线l的参数方程为 ![]() (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P(1,0).若点M的极坐标为(1, ![]() ),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com