
【题目】已知定点![]() ,动点
,动点![]() 与
与![]() 、
、![]() 两点连线的斜率之积为
两点连线的斜率之积为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知点![]() 是轨迹
是轨迹![]() 上的动点,点
上的动点,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() (其中
(其中![]() 为坐标原点),求
为坐标原点),求![]() 面积的最小值.
面积的最小值.
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() 为等比数列,求出
为等比数列,求出![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() 的前n项和
的前n项和![]() ,并判断是否存在正整数n使得
,并判断是否存在正整数n使得![]() 成立?若存在求出所有n值;若不存在说明理由.
成立?若存在求出所有n值;若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
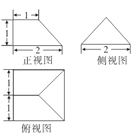
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和圆
和圆![]() 的普通方程;
的普通方程;
(2)已知直线![]() 上一点
上一点![]() ,若直线
,若直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着现代社会的发展,我国对于环境保护越来越重视,企业的环保意识也越来越强.现某大型企业为此建立了5套环境监测系统,并制定如下方案:每年企业的环境监测费用预算定为1200万元,日常全天候开启3套环境监测系统,若至少有2套系统监测出排放超标,则立即检查污染源处理系统;若有且只有1套系统监测出排放超标,则立即同时启动另外2套系统进行1小时的监测,且后启动的这2套监测系统中只要有1套系统监测出排放超标,也立即检查污染源处理系统.设每个时间段(以1小时为计量单位)被每套系统监测出排放超标的概率均为![]() ,且各个时间段每套系统监测出排放超标情况相互独立.
,且各个时间段每套系统监测出排放超标情况相互独立.
(1)当![]() 时,求某个时间段需要检查污染源处理系统的概率;
时,求某个时间段需要检查污染源处理系统的概率;
(2)若每套环境监测系统运行成本为300元/小时(不启动则不产生运行费用),除运行费用外,所有的环境监测系统每年的维修和保养费用需要100万元.现以此方案实施,问该企业的环境监测费用是否会超过预算(全年按9000小时计算)?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com