
【题目】设函数f(x)在(-∞,+∞)上有意义,且对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|并且函数f(x+1)的对称中心是(-1,0),若函数g(x)-f(x)=x,则不等式g(2x-x2)+g(x-2)<0的解集是( ).
A.![]() B.
B.![]()
C.![]() ,
,![]() D.
D.![]()
【答案】A
【解析】
由已知可知f(x)为奇函数,从而可得g(-x)也为奇函数,然后结合|f(x)-f(y)|<|x-y|,得 ![]() ,从而可得g(x)单调递增,结合单调性及奇函数的定义可求.
,从而可得g(x)单调递增,结合单调性及奇函数的定义可求.
由函数f(x+1)的对称中心是(-1,0),可得f(x)的图象关于(0,0)对称即f(x)为奇函数,
∴f(-x)=-f(x),
∵g(x)-f(x)=x,
∴g(x)=f(x)+x,
∴g(-x)=f(-x)-x=-f(x)-x=-g(x),
∵对于任意的x,y∈R,有|f(x)-f(y)|<|x-y|,
∴|g(x)-g(y)-(x-y)|<|x-y|,
∴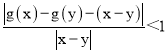 ,
,
即|![]() |<1,
|<1,
∴0<![]() <2,
<2,
由对任意实数![]() 有
有![]() 得g(x)单调递增,
得g(x)单调递增,
∵g(2x-x2)+g(x-2)<0,
∴g(2x-x2)<-g(x-2)=g(2-x),
∴2x-x2<2-x,
整理可得,x2-3x+2>0,
解可得,x>2或x<1,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数![]()
(1)证明f(x)在区间(α,β)上是增函数;
(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
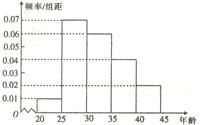
(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是![]() 和an的等差中项.
和an的等差中项.
(1)证明:数列{an}为等差数列;
(2)若bn=-n+5,求{an·bn}的最大项的值并求出取最大值时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆C过点
中,椭圆C过点![]() ,焦点
,焦点![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的方程;
(2)设直线l与圆O相切于第一象限内的点P.
①若直线l与椭圆C有且只有一个公共点,求点P的坐标;
②直线l与椭圆C交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,若
,若![]() 恒成立,则称函数
恒成立,则称函数![]() 在
在![]() 上具有“
上具有“![]() ”性质.
”性质.
(![]() )判断函数
)判断函数![]() 在
在![]() 上是否具有“
上是否具有“![]() ”性质?说明理由.
”性质?说明理由.
(![]() )若
)若![]() 在
在![]() 上具有“
上具有“![]() ”性质,求
”性质,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 棱的中点.
棱的中点.

(1)证明![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com