
【题目】已知函数f(x)=x3﹣3x2﹣9x+2.
(1)求函数f(x)的单调区间;
(2)求函数f(x)在区间[﹣1,m](m>﹣1)的最小值.
【答案】
(1)解:f′( x)=3x2﹣6x﹣9=3( x﹣3)( x+1)
令 f′( x)>0,得 x<﹣1 或 x>3
令 f′( x)<0,得﹣1<x<3
∴f( x) 的 增 区 间 为 (﹣∞,﹣1)和 ( 3,+∞),f( x) 的 减 区 间 为 (﹣1,3)
(2)解:由 ( 1)知,当﹣1<m≤3 时,
f( x)min=f( m)=m3﹣3m2﹣9m+2
当 m>3 时,f( x)min=f(3)=﹣25
∴f( x)min= 
【解析】(1)f′( x)=3x2﹣6x﹣9=3( x﹣3)( x+1),令 f′( x)>0,得 x<﹣1 或 x>3,令 f′( x)<0,得﹣1<x<3即可得到单调区间; (2)由 ( 1)知,可分当﹣1<m≤3 时,当 m>3 时分别求最小值.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且点
,且点![]() 是该函数图象的一个最高点.
是该函数图象的一个最高点.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于![]() 地的沙尘暴一直向正南方向移动,其移动速度
地的沙尘暴一直向正南方向移动,其移动速度![]() 与时间
与时间![]() 的函数图像如图所示,过线段
的函数图像如图所示,过线段![]() 上一点
上一点![]() 作横轴的垂线
作横轴的垂线![]() ,梯形
,梯形![]() 在直线
在直线![]() 左侧部分的面积即为
左侧部分的面积即为![]() 内沙尘暴所经过的路程
内沙尘暴所经过的路程![]() .
.

(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)将![]() 随
随![]() 变化的规律用数学关系式表示出来;
变化的规律用数学关系式表示出来;
(3)若![]() 城位于
城位于![]() 地正南方向,且距
地正南方向,且距![]() 地650
地650![]() ,试判断这场沙尘暴是否会侵袭到
,试判断这场沙尘暴是否会侵袭到![]() 城,如果会,在沙尘暴发生后多长时间它将侵袭到
城,如果会,在沙尘暴发生后多长时间它将侵袭到![]() 城?如果不会,请说明理由.
城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,F是PB的中点.求证:

(1)DF⊥AP.
(2)在线段AD上是否存在点G,使GF⊥平面PBC?若存在,说明G点的位置,并证明你的结论;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)
设某旅游景点每天的固定成本为500元,门票每张为30元,变动成本与购票进入旅游景点的人数的算术平方根成正比。一天购票人数为25时,该旅游景点收支平衡;一天购票人数超过100时,该旅游景点须另交保险费200元。设每天的购票人数为![]() ,盈利额为
,盈利额为![]() 元。
元。
(Ⅰ)求![]() 与
与![]() 之间的函数关系;
之间的函数关系;
(Ⅱ)该旅游景点希望在人数达到20人时即不出现亏损,若用提高门票价格的措施,则每张门票至少要多少元(取整数)?
(参考数据:![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某社区80个人,以研究这一社区居民的休闲方式是否与性别有关,得到下面的数据表:
休闲方式 | 看电视 | 运动 | 合计 |
男性 | 20 | 10 | 30 |
女性 | 45 | 5 | 50 |
合计 | 65 | 15 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人是以运动为休闲方式的人数为随机变量X,求X的分布列和期望;
(2)根据以上数据,能否有99%的把握认为休闲方式与性别有关系?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ),其中n=a+b+c+d)
),其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:

(1)E、C、D1、F、四点共面;
(2)CE、D1F、DA三线共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王先生家住 A 小区,他工作在 B 科技园区,从家开车到公司上班路上有 L1 , L2两条路线(如图),L1路线上有 A1 , A2 , A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有 B1 , B2两个路.各路口遇到红灯的概率依次为
;L2路线上有 B1 , B2两个路.各路口遇到红灯的概率依次为 ![]() ,
, ![]() .若走 L1路线,王先生最多遇到 1 次红灯的概率为;若走 L2路线,王先生遇到红灯次数 X 的数学期望为 .
.若走 L1路线,王先生最多遇到 1 次红灯的概率为;若走 L2路线,王先生遇到红灯次数 X 的数学期望为 . 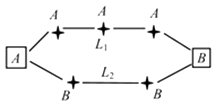
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com