
分析 (1)设出数列的公差与公比,利用已知条件列出方程,求解数列{an}的通项公式然后求解{bn}的通项公式.
(2)利用数列的通项公式,拆项,通过等差数列和等比数列分别求和即可.
解答 解:(1)设{an}的公差为d,{an+bn}的公比为q,
∴$d=\frac{{{a_4}-{a_1}}}{4-1}=-2$,∴an=a1+(n-1)d,=1+(n-1)×(-2)=-2n+3.
∵a1+b1=2,a4+b4=16,
∴${q^{4-1}}=\frac{{{a_4}+{b_4}}}{{{a_1}+{b_1}}}=8$,
∴q=2,∴${a_n}+{b_n}=2×{2^{n-1}}={2^n}$,
∴${b_n}={2^n}-{a_n}={2^n}+2n-3$.
(2)Sn=b1+b2+b3+…+bn=(21-1)+(22+1)+(23+3)+…+(2n+2n-3)
=(21+22+23+…+2n)+(-1+1+3+…+2n-3)
=$\frac{{2(1-{2^n})}}{1-2}+\frac{(-1+2n-3)n}{2}$=2n+1+n2-2n-2
点评 本题考查等差数列以及等比数列的综合应用,数列求和,考查计算能力.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:解答题
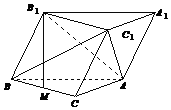 如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,M是BC的中点,且BM1⊥BC,平面B1C1CB⊥平面ABC.BC=CA=AA1.
如图,斜三棱柱ABC-A1B1C1的底面是直角三角形,∠ACB=90°,M是BC的中点,且BM1⊥BC,平面B1C1CB⊥平面ABC.BC=CA=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x>1,x2-1>0”的否定是“?x>1,x2-1≤0” | |
| B. | “x=2”是“x2-x-2=0”的充分不必要条件 | |
| C. | 若“p∧q”为假命题,则p,q均为假命题 | |
| D. | 命题“若a•b=0,则a=0或b=0”的否命题为“若a•b≠0,则a≠0且b≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?{x_0}∈R,{x_0}^2+2>0$ | B. | $?{x_0}∈R,{x_0}^2+2≤0$ | ||
| C. | $?{x_0}∈R,{x_0}^2+2<0$ | D. | ?x∈R,x2+2≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
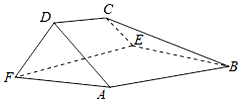 如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com