
【题目】(1)已知![]() ,
,![]() ,求函数
,求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)已知![]() ,不等式
,不等式![]() (其中
(其中![]() 为自然对数的底数)对任意的实数
为自然对数的底数)对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .极小值
.极小值![]() ,无极大值.(2)
,无极大值.(2)![]()
【解析】
(1)求导得到![]() 根据导数的正负得到函数的单调区间,再计算极值得到答案.
根据导数的正负得到函数的单调区间,再计算极值得到答案.
(2)变换得到![]() ,设
,设![]() ,等价于
,等价于![]() 即
即
![]() ,
,![]() ,根据函数的单调性得到最值得到答案.
,根据函数的单调性得到最值得到答案.
(1)函数的定义域为![]() ,
,![]() ,由
,由![]() 得,
得,![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
所以当![]() 时,
时,![]() 取得极小值
取得极小值![]() ,无极大值.
,无极大值.
(2)由![]() 得,
得,![]() ,
,
即![]() ,设
,设![]() ,
,![]() ,
,
则不等式![]() 对于任意的实数
对于任意的实数![]() 恒成立,等价于
恒成立,等价于![]() ,
,
由(1)知,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以![]() ,即
,即![]() 对任意的实数
对任意的实数![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() ,
,
即![]() 对任意的实数
对任意的实数![]() 恒成立,即
恒成立,即![]() .
.
令![]() ,则
,则![]() ,由
,由![]() 得,
得,![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上为减函数,
上为减函数,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
所以![]() ,即
,即![]() .
.
又由已知得![]() ,所以,实数
,所以,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,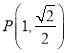 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 、直线
、直线![]() 于
于![]() 、
、![]() 两点,当
两点,当![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 的一个顶点
的一个顶点![]() 的坐标为
的坐标为![]() .过椭圆
.过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() (
(![]() ,
,![]() 不同于点
不同于点![]() ),直线
),直线![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的方程,并求点
的方程,并求点![]() 的坐标;
的坐标;
(2)求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位? 某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
考试平均成绩是![]() 分,
分,![]() 分及其以上的高分考生
分及其以上的高分考生![]() 名.
名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为![]() 分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:(1)当![]() 时,令
时,令![]() ,则
,则![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
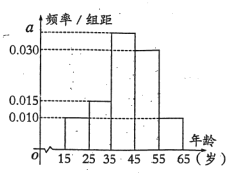
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).
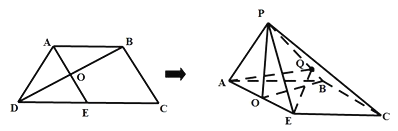
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试判断线段
,试判断线段![]() 上是否存在一点
上是否存在一点![]() (不含端点),使得直线
(不含端点),使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com