
【题目】如图所示,正方体![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱![]() 的中点,过直线
的中点,过直线![]() 的平面分别与棱
的平面分别与棱![]() 交于
交于![]() ,设
,设![]() ,
, ![]() ,给出以下四个命题:
,给出以下四个命题:
①![]()
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
, ![]() ,则
,则![]() 是奇函数;
是奇函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
其中正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,构成四面体
,构成四面体![]() ,则在四面体
,则在四面体![]() 中,下列说法不正确的是( ).
中,下列说法不正确的是( ).


A. 直线![]() 直线
直线![]() B. 直线
B. 直线![]() 直线
直线![]()
C. 直线![]() 平面
平面![]() D. 平面
D. 平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)已知a,b,c是△ABC三边长,且f(C)=2,△ABC的面积S=![]() ,c=7.求角C及a,b的值.
,c=7.求角C及a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sinxcosx将 f(x)的图象向右平移 ![]() (0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x=
(0<φ<π) 个单位,得到y=g(x)图象且g(x)的一条对称轴是直线x= ![]() .
.
(1)求φ;
(2)求函数y=g(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为公差不为
为公差不为![]() 的等差数列,
的等差数列, ![]() 为前
为前![]() 项和,
项和, ![]() 和
和![]() 的等差中项为
的等差中项为![]() ,且
,且![]() .令
.令![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)求![]() 及
及![]() ;
;
(2)是否存在正整数![]() 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 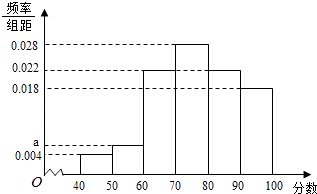
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π),在同一周期内,当x= ![]() 时,f(x)取得最大值3;当x=
时,f(x)取得最大值3;当x= ![]() 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com