
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:![]() ),经统计,其高度均在区间
),经统计,其高度均在区间![]() 内,将其按
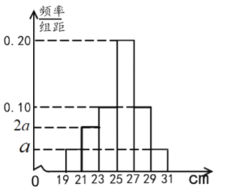
内,将其按![]() 分成6组,制成如图所示的频率分布直方图.其中高度为
分成6组,制成如图所示的频率分布直方图.其中高度为![]() 及以上的树苗为优质树苗.
及以上的树苗为优质树苗.
|
| 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
(1)求图中![]() 的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
的值,并估计这批树苗高度的中位数和平均数(同一组数据用该组区间的中点值作代表);
(2)已知所抽取的这120棵树苗来自于![]() ,
,![]() 两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有
两个试验区,部分数据如上列联表:将列联表补充完整,并判断是否有![]() 的把握认为优质树苗与
的把握认为优质树苗与![]() ,
,![]() 两个试验区有关系,并说明理由.
两个试验区有关系,并说明理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
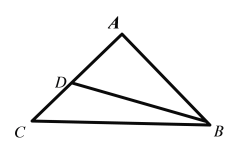
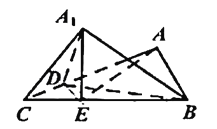
【题目】如图,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,D为AC上一点,将
,D为AC上一点,将![]() 沿BD折起,得到三棱锥
沿BD折起,得到三棱锥![]() ,且使得
,且使得![]() 在底面BCD的投影E在线段BC上,连接AE.
在底面BCD的投影E在线段BC上,连接AE.
(1)证明:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,设圆
,设圆![]() 与圆
与圆![]() 的公共弦所在直线为
的公共弦所在直线为![]() .
.
(1)求直线![]() 的极坐标方程;
的极坐标方程;
(2)若以坐标原点为中心,直线![]() 顺时针方向旋转
顺时针方向旋转![]() 后与圆
后与圆![]() 、圆
、圆![]() 分别在第一象限交于
分别在第一象限交于![]() 、
、![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:

(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(ⅰ)若日需求量为15个,求![]() ;
;
(ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: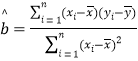
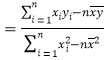 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学物理分数对应如下表:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学分数 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分数 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
绘出散点图如下:

根据以上信息,判断下列结论:
①根据此散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据此散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③甲同学数学考了80分,那么,他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高.
其中正确的个数为( ).
A.0B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD是直角梯形,∠DAB=90°AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2,BC![]() ,E是线段AB的中点.
,E是线段AB的中点.
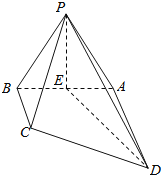
(1)求证:PE⊥CD;
(2)求PC与平面PDE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com