Question

【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 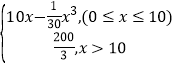其中x(单位:万件)是年产量.

(1)写出年利润W(单位:万元)关于年产量x的函数解析式.

(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?

Answer 1

【答案】（1）见解析（2）9

【解析】

（1）依据利润的计算方法，即利润=销售收入﹣投入，直接写出年利润函数即可．

（2）分类讨论：当0≤x≤10时；当x＞10时，分别求出分段上各个函数的最大值，最后综合得出当年产量为多少万件，公司所获得的利润最大即可．

解:(1)依题意有,W=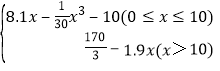

(2) 当0≤x≤10时，∵W（x）=∴W′（x）=

令W′（x）=0，解得x=9．

若0≤x＜9，则W′（x）＞0；若9＜x≤10，则W′（x）＜0，

∴W（x）的最大值为W（9）=38.6．

当x＞10时，W（x）=．

综上可知，当x=9时W（x）的最大值为W（9）=38.6

答：当年产量为9万件，公司所获得的利润最大