
| j |
| OA |
| j |
| AB |
A. | B. | C. | D. |
科目:高中数学 来源:不详 题型:单选题
| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A.
| B.
| ||||||||||||||||||||||||||||
C.
| D.
|
查看答案和解析>>
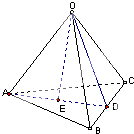
科目:高中数学 来源:不详 题型:解答题
| AC |
| DE |
| AP |
查看答案和解析>>
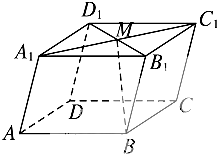
科目:高中数学 来源:不详 题型:填空题
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线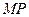 、
、 分别交
分别交 轴于点
轴于点 和点
和点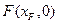 ,
, 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;  时,
时, 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,  的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关; 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com