
����Ŀ��ijѧУΪ����ȫ��ѧ��Ϊ����ѧ����������һԪǮ��һƬ�ģ�������ˮ�����ѧ���ڹ�ˮ��ÿ��ȡһƿ��Ȫˮ�����Ծ�������������Ͷ��һԪǮ����ͳ��������5����۳���������������±���
�۳�ˮ��x����λ���䣩 | 7 | 6 | 6 | 5 | 6 |
����y����λ��Ԫ�� | 165 | 142 | 148 | 125 | 150 |
(��) ��x��y��������أ���ij���۳�8��ˮʱ��Ԥ������Ϊ����Ԫ��
(��) ���п����Ժ�ѧУ������������ˮ�����棬�Խ�ѧ�����ʽ������Ʒѧ���ŵ����������涨�������������꼶ǰ200������һ�Ƚ�ѧ��500Ԫ�������꼶201��500 ��������Ƚ�ѧ��300Ԫ�������꼶501���Ժ��������������ý�ѧ�𡣼ס�������ѧ����һ�Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������Ƚ�ѧ��ĸ��ʾ�Ϊ
������Ƚ�ѧ��ĸ��ʾ�Ϊ![]() ������ý�ѧ��ĸ��ʾ�Ϊ
������ý�ѧ��ĸ��ʾ�Ϊ![]() .
.
����ѧ����ý�ѧ�������£��������һ�Ƚ�ѧ��ĸ��ʣ�
����֪�ס�������ѧ������ĸ��ȵڵĽ�ѧ����������ģ���ס�������ѧ������ý�ѧ���ܽ��X �ķֲ��м���ѧ������
���� 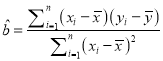 ��
�� ![]() ��
��
���𰸡�����186Ԫ������1��![]() ����2���ֲ��м�����������Ϊ600.
����2���ֲ��м�����������Ϊ600.
�����������������
(��)���������ûع鷽��Ϊ![]() ���ݴ�Ԥ���۳�8��ˮʱ��Ԥ������Ϊ186Ԫ��
���ݴ�Ԥ���۳�8��ˮʱ��Ԥ������Ϊ186Ԫ��
(��) (1)���������ʹ�ʽ�ɵ������һ�Ƚ�ѧ��ĸ�����![]() ��
��
(2) ������ɵ�X��ȡֵ����Ϊ0��300��500��600��800��1000���ݴ���÷ֲ��У�Ȼ�����ɵ���ѧ����Ϊ600.
���������
![]() ��
�� ![]()
 ��
�� ![]()
![]() ��
��
��![]() ʱ��
ʱ�� ![]()
��ij���۳�8��ˮ��Ԥ��������186Ԫ��
(��) �����¼�AΪ��ѧ����ý�ѧ�������¼�BΪ��ѧ�����һ�Ƚ�ѧ������

��ѧ����ý�ѧ��������£����һ�Ƚ�ѧ��ĸ���Ϊ![]()
��X��ȡֵ����Ϊ0��300��500��600��800��1000
![]() ��
��![]() ��
��![]()
![]() ��
��![]() ��
��![]()
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��

![]() ��Ԫ��
��Ԫ��


 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д� �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ���Ҷ���Ϊ
���Ҷ���Ϊ![]() .��֪
.��֪![]() ������
������![]() Ϊԭ�㣬
Ϊԭ�㣬 ![]() Ϊ��Բ��������.
Ϊ��Բ��������.
��1������Բ�ķ��̼�������![]() ��ֵ��
��ֵ��
��2�������![]() ��ֱ��
��ֱ��![]() ����Բ���ڵ�
����Բ���ڵ�![]() ��
��![]() ����
����![]() ���ϣ�����ֱ��
���ϣ�����ֱ��![]() ��ֱ����
��ֱ����![]() ���ڵ�
���ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() .��
.��![]() ����
����![]() ����ֱ��
����ֱ��![]() ��б�ʵ�ȡֵ��Χ.
��б�ʵ�ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ��ΪC��Բ������A��0��2����B��1��1������Բ��C��ֱ��l��x+y+5=0�ϣ�
��1����ԲC�ı����̣�
��2����P��x��y����ԲC�ϵĶ��㣬��3x��4y�����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��������![]() ʱ����
ʱ����![]() �ļ�ֵ��
�ļ�ֵ��
����![]() ʱ������
ʱ������![]() �ĵ����ԣ�
�ĵ����ԣ�
�����������������![]() ����
����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У���ԭ��OΪ���㣬��x��������Ϊ���ᣬ����C�ļ����귽��Ϊ��= ![]() �� ��������C�ļ����귽�̻�Ϊֱ�����귽�̣�
�� ��������C�ļ����귽�̻�Ϊֱ�����귽�̣�
������P��0��2����б��Ϊ1ֱ��l������C����A��B���㣬���� ![]() +
+ ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���б��Ϊ1��2��3�����������Ϊ4��5��6���������������������ź���ɫ����ȫ��ͬ���ִ�������ȡ��������
��1����ȡ�õ���������ɫ��ͬ�ĸ��ʣ�
��2����ȡ�õ���������ɫ����ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() �DZ߳�Ϊ2��������
�DZ߳�Ϊ2��������![]() ��
��![]() �ߵ��е㣬��
�ߵ��е㣬��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ����ʹ�õ�
����ʹ�õ�![]() ���
���![]() �غϣ���Ϊ��
�غϣ���Ϊ��![]() ���õ�����
���õ�����![]() ��
��
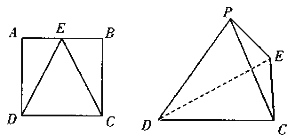
������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
�������![]() ��ƽ��
��ƽ��![]() �ľ��룮
�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵õ�����y=2sin��2x+ ![]() ����ͼ��ֻ��Ѻ���y=2sinx��ͼ�� ��
����ͼ��ֻ��Ѻ���y=2sinx��ͼ�� ��
A.����ƽ�� ![]() ����λ���ȣ��ٰ����ø���ĺ������Ϊԭ����2���������겻�䣩
����λ���ȣ��ٰ����ø���ĺ������Ϊԭ����2���������겻�䣩
B.����ƽ�� ![]() ����λ���ȣ��ٰ����ø���ĺ������Ϊԭ����
����λ���ȣ��ٰ����ø���ĺ������Ϊԭ���� ![]() ���������겻�䣩
���������겻�䣩
C.����������겻�䡢�������Ϊԭ����2�����ٰ�����ͼ������ƽ�� ![]() ����λ����
�������
D.����������겻�䡢�������Ϊԭ���� ![]() �����ٰ�����ͼ������ƽ��
�����ٰ�����ͼ������ƽ�� ![]() ����λ����
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ��
��![]() �����ҽ�����ֱ��
�����ҽ�����ֱ��![]() ��
�� ![]() �ϣ�����Բ��������������ԭ��ԳƵĵ�����Բ������һ������ߵ�б��֮��Ϊ
�ϣ�����Բ��������������ԭ��ԳƵĵ�����Բ������һ������ߵ�б��֮��Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ������
������![]() ��������Բ
��������Բ![]() ����������
����������![]() ��
�� ![]() ���Ƿ����ֱ��
���Ƿ����ֱ��![]() ��
�� ![]() ������
������![]() ��ʹ��
��ʹ��![]() ��
�� ![]() ��
��![]() �ľ���
�ľ���![]() ��
�� ![]() ����
����![]() ������������ڣ����
������������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com