练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】直线mx+ y﹣1=0在y轴上的截距是﹣1，且它的倾斜角是直线 =0的倾斜角的2倍，则（ ）
    A.m=﹣ ，n=﹣2
    B.m= ，n=2
    C.m= ，n=﹣2
    D.m=﹣ ，n=2

    【答案】A
    【解析】解：根据题意，设直线mx+ y﹣1=0为直线l，

    另一直线的方程为 =0，

    变形可得y= （x﹣3），其斜率k= ，

    则其倾斜角为60°，

    而直线l的倾斜角是直线 =0的倾斜角的2倍，

    则直线l的倾斜角为120°，

    且斜率k=tan120°=﹣ ，

    又由l在y轴上的截距是﹣1，则其方程为y=﹣ x﹣1；

    又由其一般式方程为mx+ y﹣1=0，

    分析可得：m=﹣ ，n=﹣2；

    所以答案是：A．

    【考点精析】通过灵活运用斜截式方程，掌握直线的斜截式方程：已知直线的斜率为，且与轴的交点为则：即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对于函数f（x）=xlnx有如下结论： ①该函数为偶函数；
    ②若f′（x0）=2，则x0=e；
    ③其单调递增区间是[ ，+∞）；
    ④值域是[ ，+∞）；
    ⑤该函数的图象与直线y=﹣ 有且只有一个公共点．（本题中e是自然对数的底数）
    其中正确的是（请把正确结论的序号填在横线上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】①用反证法证明：在一个三角形中，至少有一个内角大于或等于60°；
    ②已知 ，试用分析法证明：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞2，求证：loga(a－1)＜log(a＋1)a.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列 的首项 ，前n项和为 ，且 .
    （1）证明数列 是等比数列；
    （2）令 ，求函数 在点x＝1处的导数 ，并比较 与 的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱A1B1C1﹣ABC中，AB=AC=AA1 ， ，点D是BC的中点．
    （I）求证：AD⊥平面BCC1B1；
    （II）求证：A1B∥平面ADC1；
    （III）求二面角A﹣A1B﹣D的余弦值．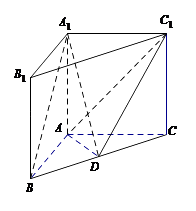

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=﹣ +4x﹣3lnx在[t，t+1]上不单调，则t的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为对本公司的160名员工的身体状况进行调查，先将员工随机编号为1，2，3，…，159，160，采用系统抽样的方法（等间距地抽取，每段抽取一个个体）将抽取的一个样本．已知抽取的员工中最小的两个编号为5，21，那么抽取的员工中，最大的编号应该是（ ）
    A.141
    B.142
    C.149
    D.150

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣alnx（a∈R）
    （1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
    （2）求函数f（x）的极值．

    查看答案和解析>>

    同步练习册答案