
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
分析 基本事件总数N=3×2=6,函数y=mx+n是增函数需要满足的条件是m>0,从而求出函数y=mx+n是增函数包含的基本事件个数,由此能求出函数y=mx+n是增函数的概率.
解答 解:∵关于x的一次函数y=mx+n,设m∈{-1,1,2},n∈{-2,2},
∴基本事件总数N=3×2=6,
函数y=mx+n是增函数需要满足的条件是m>0,
∴函数y=mx+n是增函数包含的基本事件个数M=2×2=4,
∴函数y=mx+n是增函数的概率p=$\frac{M}{N}=\frac{4}{6}=\frac{2}{3}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
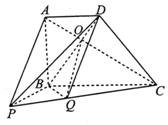 如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.
如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{10}}}{20}$ | B. | $\frac{{\sqrt{10}}}{20}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥$\frac{1}{5}$ | B. | a>$\frac{1}{5}$ | C. | a<$\frac{1}{5}$ | D. | a≤$\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤1} | B. | {x|-1≤x<2} | C. | {x|-1≤x<0} | D. | {x|1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com