
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() ,E为PD的中点,
,E为PD的中点,![]() ,
,![]() .
.
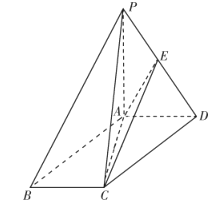
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左右顶点分别是
的左右顶点分别是![]() ,离心率为
,离心率为![]() ,设点
,设点![]() ,连接
,连接![]() 交椭圆于点
交椭圆于点![]() ,坐标原点是
,坐标原点是![]() .
.

(1)证明: ![]() ;
;
(2)设三角形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() , 若
, 若 ![]() 的最小值为1,求椭圆的标准方程.
的最小值为1,求椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() 是
是![]() 与
与![]() 的等差中项;②
的等差中项;②![]() 是
是![]() 与
与![]() 的等比中项;③数列
的等比中项;③数列![]() 的前5项和为65这三个条件中任选一个,补充在横线中,并解答下面的问题.
的前5项和为65这三个条件中任选一个,补充在横线中,并解答下面的问题.
已知![]() 是公差为2的等差数列,其前
是公差为2的等差数列,其前![]() 项和为
项和为![]() ,________________________.
,________________________.
(1)求![]() ;
;
(2)设![]() ,是否存在
,是否存在![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形,![]() ,若棱
,若棱![]() ,
,![]() ,
,![]() 两两垂直,长度分别为1,2,2,且向量
两两垂直,长度分别为1,2,2,且向量![]() 与
与![]() 夹角的余弦值为
夹角的余弦值为![]() .
.
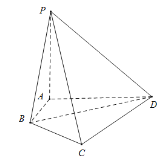
(1)求![]() 的长度;
的长度;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解城市道路交通压力,促进城市道路交通有序运转,减少机动车尾气排放对空气质量的影响,西安市人民政府决定:自2019年3月18日至2020年3月13日在相关区域实施工作日机动车尾号限行交通管理措施.已知每辆机动车每周一到周五都要限行一天,周末(周六和周日)不限行.某公司有A,B,C,D,E五辆车,每天至少有四辆车可以上路行驶.已知E车周四限行,B车昨天限行,从今天算起,A,C 两辆车连续四天都能上路行驶,E车明天可以上路,由此可知下列推测一定正确的是( )
A.今天是周四B.今天是周六C.A车周三限行D.C车周五限行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系内,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 和直线
和直线![]() 化为直角坐标方程;
化为直角坐标方程;
(2)过原点![]() 引一条射线分别交曲线
引一条射线分别交曲线![]() 和直线
和直线![]() 于
于![]() ,
,![]() 两点,射线上另有一点
两点,射线上另有一点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程(写成直角坐标形式的普通方程).
的轨迹方程(写成直角坐标形式的普通方程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知圆![]() 和圆
和圆![]() 的极坐标方程分别是
的极坐标方程分别是![]() 和
和![]() .
.
(1)求圆![]() 和圆
和圆![]() 的公共弦所在直线的直角坐标方程;
的公共弦所在直线的直角坐标方程;
(2)若射线![]() :
:![]() 与圆
与圆![]() 的交点为O、P,与圆
的交点为O、P,与圆![]() 的交点为O、Q,求
的交点为O、Q,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com