
分析 对任意的x2∈[$\frac{1}{e}$,1],存在${x_1}∈[\frac{1}{e},1]$,f(x1)≥g(x2)成立?f(x1)min≥g(x2)min,先对函数g(x)求导判断出函数g(x)的单调性并求其最小值,然后对函数f(x)进行求导判断单调性求其最小值,即可.
解答 解:∵g(x)=x-lnx
∴g'(x)=1-$\frac{1}{x}$,x∈[$\frac{1}{e}$,1],g'(x)≤0,函数g(x)单调递减,g(x)的最小值为g(1)=1,
f'(x)=$\frac{{x}^{2}-{a}^{2}}{{x}^{2}}$,令f'(x)=0∵a>0∴x=a
当a≥1时,f(x)在[$\frac{1}{e}$,1],上单调减,f(x)最小=f(1)=1+a2≥1恒成立,符合题意;
当$\frac{1}{e}<a<1$时,在[$\frac{1}{e}$,a]上单调减,在[a,1],上单调增,f(x)最小=f(a)=2a≥1,⇒$\frac{1}{2}≤a<1$;
当a$≤\frac{1}{e}$时,在[$\frac{1}{e}$,1]上单调增,f(x)最小=f($\frac{1}{e}$)=$\frac{1}{e}+{a}^{2}e≥1$,⇒$\frac{\sqrt{{e}^{2}-1}}{e}≤a≤\frac{1}{e}$
综上:则实数a的取值范围是:[$\frac{1}{2}$,+∞)∪[$\frac{\sqrt{{e}^{2}-1}}{e}$,$\frac{1}{e}$].
故答案为:[$\frac{1}{2}$,+∞)∪[$\frac{\sqrt{{e}^{2}-1}}{e}$,$\frac{1}{e}$].
点评 本题主要考查了关任意性和存在性问题的转化策略,将任意性与存在性问题转化为函数值域关系或最值关系,并得到双变量的存在性和任意性问题的辨析方法,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{10},10)$ | B. | (0,10) | C. | (10,+∞) | D. | $(0,\frac{1}{10})∪(10,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | $\sqrt{3}$-1 | C. | $\sqrt{5}$-2 | D. | $\sqrt{6}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
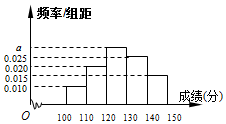 某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.
某学校对高二年级期中考试数学成绩进行分析,随机抽取了分数在[100,150]的1000名学生的成绩,并根据这1000名学生的成绩画出频率分布直方图(如图所示),则成绩在[120,130)内的学生共有300人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<1} | B. | {x|x>1} | C. | {x|-1<x<1} | D. | {x|x≥-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com