
【题目】已知点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 方程;
方程;
(2)动直线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,且
,且![]() 的面积为
的面积为![]() ,其中
,其中![]() 为坐标原点,证明
为坐标原点,证明![]() 为定值.
为定值.
【答案】(1)![]() (2)证明见解析;
(2)证明见解析;
【解析】
(1)设![]() ,根据点
,根据点![]() 在线段
在线段![]() 上,且
上,且![]() ,得到
,得到![]() ,
,![]() 的坐标,再由
的坐标,再由![]() 建立x,y方程即可所求.
建立x,y方程即可所求.
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,根据
轴对称,根据![]() 在椭圆上和
在椭圆上和![]() ,求得坐标即可,当直线
,求得坐标即可,当直线![]() 的斜率存在时,设直线方程为
的斜率存在时,设直线方程为![]() ,将
,将![]() 代入方程
代入方程![]() 中,利用弦长公式求得
中,利用弦长公式求得![]() ,点
,点![]() 到直线
到直线![]() 的距离,由
的距离,由![]() 得到k,m的关系,再利用韦达定理求解即可.
得到k,m的关系,再利用韦达定理求解即可.
(1)设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,
所以![]() ,
,![]() ,
,
因为![]() ,
,
所以![]() ,
,
即![]() ,
,
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,
轴对称,
所以![]() ,
,![]() .
.
因为![]() ,在椭圆上,所以有
,在椭圆上,所以有![]() ,
,
又因为![]() ,
,
所以![]() ,
,
解得![]() ,
,![]() ,
,
此时![]() ,
,![]() ,
,
![]()
②当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,由题意
,由题意![]() .
.
将![]() 代入方程
代入方程![]() 中,
中,
整理得![]() ,
,
![]() ①
①
![]() ,
,![]() ,
,
则![]() .
.
因为点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]() ,
,
得![]() 且符合①式,
且符合①式,
此时![]() ,
,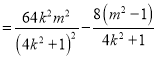
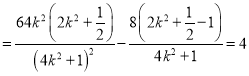 ,
,
![]() ,
,
所以![]() ,
,
综上所述,![]() (定值)
(定值)


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】某中学举行了科学防疫知识竞赛.经过选拔,甲、乙、丙三位选手进入了最后角逐.他们还将进行四场知识竞赛.规定:每场知识竞赛前三名的得分依次为a,b,c(![]() ,且a,b,
,且a,b,![]() );选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
);选手总分为各场得分之和.四场比赛后,已知甲最后得分为16分,乙和丙最后得分都为8分,且乙只有一场比赛获得了第一名,则下列说法正确的是( )
A.每场比赛的第一名得分a为4
B.甲至少有一场比赛获得第二名
C.乙在四场比赛中没有获得过第二名
D.丙至少有一场比赛获得第三名
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P ABC中,PA⊥平面ABC,![]() Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为
Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为![]() 则该三棱锥外接球的表面积为( )
则该三棱锥外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解该校学生“停课不停学”的网络学习效率,随机抽查了高一年级100位学生的某次数学成绩,得到如图所示的频率分布直方图:
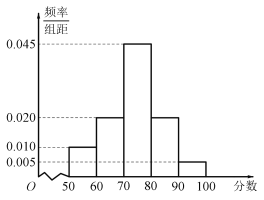
(1)估计这100位学生的数学成绩的平均值![]() .(同一组中的数据用该组区间的中点值代表);
.(同一组中的数据用该组区间的中点值代表);
(2)根据整个年级的数学成绩,可以认为学生的数学成绩![]() 近似地服从正态分布
近似地服从正态分布![]() 经计算,(1)问中样本标准差
经计算,(1)问中样本标准差![]() 的近似值为10.用样本平均数
的近似值为10.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
参考数据:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]()
(3)该年级1班的数学老师为了能每天督促学生的网络学习,提高学生每天的作业质量及学习数学的积极性,特意在微信上设计了一个每日作业小程序,每当学生提交的作业获得优秀时,就有机会参与一次小程序中“玩游戏,得奖励积分”的活动,开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格,共15格,刚开始有只小兔子在第1格,每点一下游戏的开始按钮,小兔子就沿着方格跳一下,每次跳1格或跳2格,概率均为![]() ,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第
,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() 的值.(获胜的概率)
的值.(获胜的概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
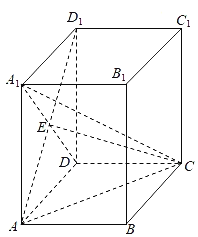
(1)证明:AE⊥平面ECD.
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国古代数学家、天文学家,大约公元222年,赵爽为《周碑算经》一书作序时,介绍了“勾股圆方图”,又称“赵爽弦图”(以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的,如图(1)),类比“赵爽弦图”,可类似地构造如图(2)所示的图形,它是由3个全等的三角形与中间的一个小正三角形组成的一个大正三角形,设![]() ,若在大正三角形中随机取一点,则此点取自小正三角形的概率为( )
,若在大正三角形中随机取一点,则此点取自小正三角形的概率为( )
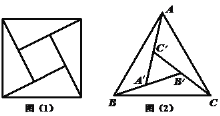
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知四边形AA1C1C为矩形,AA1=6,AB=AC=4,∠BAC=∠BAA1=60°,∠A1AC的角平分线AD交CC1于D.
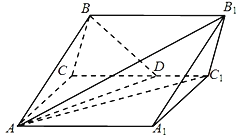
(1)求证:平面BAD⊥平面AA1C1C;
(2)求二面角A﹣B1C1﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥P﹣ABCD的底面边长为2,侧棱长为2![]() ,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
,过点A作一个与侧棱PC垂直的平面α,则平面α被此正四棱锥所截的截面面积为_____,平面α将此正四棱锥分成的两部分体积的比值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com