
【题目】已知x,y,z∈(0,+∞),x+y+z=3.
(1)求![]() 的最小值;
的最小值;
(2)证明:![]()
【答案】(1)3;(2)![]()
【解析】
(1)根据基本不等式:x+y+z≥3![]() ﹣﹣﹣﹣﹣①;
﹣﹣﹣﹣﹣①;![]() +
+![]() +
+![]() ≥3
≥3![]() ﹣﹣﹣﹣﹣②;再两式同向相乘即可.
﹣﹣﹣﹣﹣②;再两式同向相乘即可.
(2)构造柯西不等式:(12+12+12)(x2+y2+z2)=3(x2+y2+z2)≥(x+y+z)2这个条件进行计算即可.
(1) 因为x>0,y>0,z>0,根据基本不等式:
x+y+z≥3![]() ﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
![]() +
+![]() +
+![]() ≥3
≥3![]() ﹣﹣﹣﹣﹣﹣﹣﹣﹣②
﹣﹣﹣﹣﹣﹣﹣﹣﹣②
①②两式同向相乘得,
(x+y+z)(![]() +
+![]() +
+![]() )≥(3
)≥(3![]() )(3
)(3![]() )=9,
)=9,
所以,![]() +
+![]() +
+![]() ≥
≥![]() =3,
=3,
当且仅当:x=y=z=1时,原式取得最小值,
即![]() +
+![]() +
+![]() 的最小值为3.
的最小值为3.
(2) 由柯西不等式可得(12+12+12)(x2+y2+z2)≥(x+y+z)2=9,
可得:x2+y2+z2≥3,
即x2+y2+z2的最小值为3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表
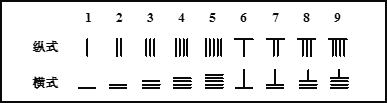
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推, 例如6613用算筹表示就是:![]() ,则26337用算筹可表示为( )
,则26337用算筹可表示为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在第三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有( )
A.12种B.24种C.36种D.48种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工健康工作,在全校范围内倡导“每天一万步”健步走活动,学校界定一人一天走路不足4千步为健步常人,不少于16千步为健步超人,其他为健步达人,学校随机抽查了36名教职工,其每天的走步情况统计如下:
步数 |
|
|
|
人数 | 6 | 18 | 12 |
现对抽查的36人采用分层抽样的方式选出6人
(1)求从这三类人中各抽多少人;
(2)现从选出的6人中随机抽取2人,求这两人健步类型相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子,他提出了一条原原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高。这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等。设由椭圆![]() 所围成的平面图形绕
所围成的平面图形绕![]() 轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
轴旋转一周后,得一橄榄状的几何体(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
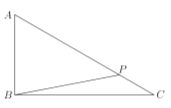
【题目】如图,某公园有三个警卫室![]() 、
、![]() 、
、![]() 有直道相连,
有直道相连,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
(1)保安甲沿![]() 从警卫室
从警卫室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的直线距离;
的直线距离;
(2)保安甲沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,同时保安乙沿
,同时保安乙沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用合适的方法表示下列集合,并说明是有限集还是无限集.
(1)到A、B两点距离相等的点的集合
(2)满足不等式![]() 的
的![]() 的集合
的集合
(3)全体偶数
(4)被5除余1的数
(5)20以内的质数
(6)![]()
(7)方程![]() 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com