练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四棱锥P﹣ABCD中， =（4，﹣2，3）， =（﹣4，1，0）， （﹣6，2，﹣8），则该四棱锥的高为 ．

    【答案】2
    【解析】解：四棱锥P﹣ABCD中， =（4，﹣2，3）， =（﹣4，1，0）， （﹣6，2，﹣8），
    设平面ABCD的法向量为 =（x，y，z），
    则 ，
    可得 ，
    不妨令x=3，则y=12，z=4，
    可得 =（3，12，4）；
    则 =（﹣6，2，﹣8）在平面ABCD上的射影就是这个四棱锥的高h，
    所以h=| ||cos＜ ， ＞|=| |= =2；
    所以该四棱锥的高为2．
    所以答案是：2．
    【考点精析】解答此题的关键在于理解棱锥的结构特征的相关知识，掌握侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】解不等式：0≤x2﹣x﹣2≤4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求函数的单调区间；

    （2）若函数既有一个极小值又有一个极大值，求的取值范围；

    （3）若存在，使得当时， 的值域是，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆x2+y2﹣2x+4y+3=0的圆心到直线x﹣y=1的距离为：（ ）
    A.2
    B.
    C.1
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某老师对全班名学生学习积极性和参加社团活动情况进行调查，统计数据如下所示：

    参加社团活动

    不参加社团活动

    合计

    学习积极性高

    学习积极性一般

    合计

    （1）请把表格数据补充完整；

    （2）若从不参加社团活动的人按照分层抽样的方法选取人，再从所选出的人中随机选取两人作为代表发言，求至少有一个学习积极性高的概率；

    （3）运用独立性检验的思想方法分析：请你判断是否有的把握认为学生的学习积极性与参与社团活动由关系？

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题p：函数f（x）= （a＞0，且a≠1）在R上为单调递减函数，命题q：x∈[0， ]，x2﹣a≤0恒成立．
    （1）求命题q真时a的取值范围；
    （2）若命题p∧q为假，p∨q为真，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】平面直角坐标系中，椭圆： （）的离心率是，抛物线： 的焦点是的一个顶点．

    （1）求椭圆的方程；

    （2）设是上动点，且位于第一象限， 在点处的切线与交于不同的两点， ，线段的中点为，直线与过且垂直于轴的直线交于点．

    （i）求证：点在定直线上；

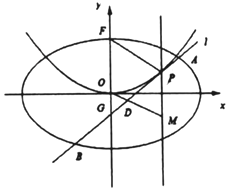
    （ii）直线与轴交于点，记的面积为， 的面积为，求的最大值及取得最大值时点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥中，四边形是菱形， ，又平面,

    点是棱的中点， 在棱上，且.

    （1）证明：平面平面；

    （2）若平面，求四棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数
    （1）若m=1，求函数f（x）的定义域．
    （2）若函数f（x）的值域为R，求实数m的取值范围．
    （3）若函数f（x）在区间 上是增函数，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案