
【题目】通过随机询问![]() 名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 |
|
|
|
不读营养说明 |
|
|
|
总计 |
|
|
|
附:
|
|
|
|
|
|
|
|
![]()
(1)由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为性别和是否看营养说明有关系呢?
的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的![]() 名不读营养说明的大学生中随机选取
名不读营养说明的大学生中随机选取![]() 名学生,求抽到女生人数
名学生,求抽到女生人数![]() 的分布列及数学期望.
的分布列及数学期望.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】秸秆还田是当今世界上普通重视的一项培肥地力的增产措施,在杜绝了秸秆焚烧所造成的大气污染的同时还有增肥增产作用.某农机户为了达到在收割的同时让秸秆还田,花![]() 元购买了一台新型联合收割机,每年用于收割可以收入
元购买了一台新型联合收割机,每年用于收割可以收入![]() 万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用
万元(已减去所用柴油费);该收割机每年都要定期进行维修保养,第一年由厂方免费维修保养,第二年及以后由该农机户付费维修保养,所付费用![]() (元)与使用年数
(元)与使用年数![]() 的关系为:
的关系为:![]() ,已知第二年付费
,已知第二年付费![]() 元,第五年付费
元,第五年付费![]() 元.
元.
(1)试求出该农机户用于维修保养的费用![]() (元)与使用年数
(元)与使用年数![]() 的函数关系;
的函数关系;
(2)这台收割机使用多少年,可使平均收益最大?(收益=收入-维修保养费用-购买机械费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道,函数![]() 的图象关于坐标原点成中心对称图形的充要条件是函数
的图象关于坐标原点成中心对称图形的充要条件是函数![]() 为奇函数,有同学发现可以将其推广为:函数
为奇函数,有同学发现可以将其推广为:函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形的充要条件是函数
成中心对称图形的充要条件是函数![]() 为奇函数.
为奇函数.
(1)求函数![]() 图象的对称中心;
图象的对称中心;
(2)类比上述推广结论,写出“函数![]() 的图象关于y轴成轴对称图形的充要条件是函数
的图象关于y轴成轴对称图形的充要条件是函数![]() 为偶函数”的一个推广结论.
为偶函数”的一个推广结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对于定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”.下列结论中正确的个数为( )
特征函数”.下列结论中正确的个数为( )
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”.
特征函数”.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
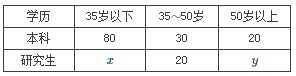
(1)用分层抽样的方法在![]() 岁年龄段的专业技术人员中抽取一个容量为
岁年龄段的专业技术人员中抽取一个容量为![]() 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取![]() 人,求至少有
人,求至少有![]() 人的学历为研究生的概率;
人的学历为研究生的概率;
(2)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取![]() 个人,其中
个人,其中![]() 岁以下
岁以下![]() 人,
人,![]() 岁以上
岁以上![]() 人,再从这
人,再从这![]() 个人中随机抽取出
个人中随机抽取出![]() 人,此人的年龄为
人,此人的年龄为![]() 岁以上的概率为
岁以上的概率为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ( x R ,且 e 为自然对数的底数).
( x R ,且 e 为自然对数的底数).
⑴ 判断函数 f x 的单调性与奇偶性;
⑵是否存在实数 t ,使不等式![]() 对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
对一切的 x R 都成立?若存在,求出 t 的值,若 不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
(1)命题“若![]() 、
、![]() 都是奇数,则
都是奇数,则![]() 是偶数”的否命题是“若
是偶数”的否命题是“若![]() 、
、![]() 都不是奇数,则
都不是奇数,则![]() 不是偶数”;
不是偶数”;
(2)命题“如果![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(3)“![]() 或
或![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
那么其中正确的说法有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com