已知a、b是非零向量,指出下列等式成立的条件:
①|a|+|b|=|a+b|成立的条件是________;
②|a|+|b|=|a-b|成立的条件是________;
③|a+b|=|a-b|成立的条件是________;
④|a|-|b|=|a-b|成立的条件是________.

同向

反向

垂直

同向
分析:利用向量的运算法则:三角形法则得到①②④的答案;通过向量模的平方等于向量的平方及向量垂直的充要条件得到③的答案.
解答:利用向量的运算法则知
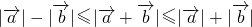
当两个向量同向时,右边的等号取得,当两个向量反向时,取得左边的等号
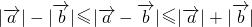
当两个向量同向时,左边的等号取得,当两个向量反向时,取得右边的等号
对于
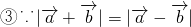
平方得

所以

垂直.
故答案为:

同向;

反向;

垂直;

同向
点评:本题考查向量的运算法则:三角形法则、考查向量模的性质:模的平方等于向量的平方、考查向量垂直的充要条件.
