
【题目】在棱长均相等的正三棱柱![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 在
在![]() 上,且
上,且![]() ,则下述结论:①
,则下述结论:①![]() ;②
;②![]() ;③平面
;③平面![]() 平面
平面![]() :④异面直线
:④异面直线![]() 与
与![]() 所成角为
所成角为![]() 其中正确命题的个数为( )
其中正确命题的个数为( )
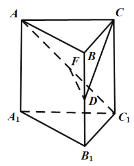
A.1B.2C.3D.4
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】给出下面类比推理:
①“若2a<2b,则a<b”类比推出“若a2<b2,则a<b”;
②“(a+b)c=ac+bc(c≠0)”类比推出“![]() (c≠0)”;
(c≠0)”;
③“a,b∈R,若a-b=0,则a=b”类比推出“a,b∈C,若a-b=0,则a=b”;
④“a,b∈R,若a-b>0,则a>b”类比推出“a,b∈C,若a-b>0,则a>b(C为复数集)”.
其中结论正确的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点在坐标轴上.
(1)若抛物线C经过点![]() ,求C的标准方程;
,求C的标准方程;
(2)抛物线C的焦点![]() (m是大于零的常数),若过点F的直线与C交于
(m是大于零的常数),若过点F的直线与C交于![]()
![]() 两点,
两点,![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于x的一元二次方程![]() .
.
(1)若a是从0、1、2、3四个数中任取的一个数,是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率.
(2)若a是从区间![]() 内任取的一个数,
内任取的一个数,![]() ,求上述方程没有实根的概率.
,求上述方程没有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十四届全国冬季运动会召开期间,某校举行了“冰上运动知识竞赛”,为了解本次竞赛成绩情况,从中随机抽取部分学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
(1)求![]() 、
、![]() 、
、![]() 的值及随机抽取一考生其成绩不低于70分的概率;
的值及随机抽取一考生其成绩不低于70分的概率;
(2)若从成绩较好的3、4、5组中按分层抽样的方法抽取5人参加“普及冰雪知识”志愿活动,并指定2名负责人,求从第4组抽取的学生中至少有一名是负责人的概率.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 15 | 0.15 |
第2组 |
| 35 | 0.35 |
第3组 |
| b | 0.20 |
第4组 |
| 20 |
|
第5组 |
| 10 | 0.1 |
合计 |
| 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是自然对数的底数)
是自然对数的底数)
(1)若![]() 在R上单调递增,求正数a的取值范围;
在R上单调递增,求正数a的取值范围;
(2)若![]() f(x)在
f(x)在![]() 处导数相等,证明:
处导数相等,证明:![]() ;
;
(3)当![]() 时,证明:对于任意
时,证明:对于任意![]() ,若
,若![]() ,则直线
,则直线![]() 与曲线
与曲线![]() 有唯一公共点(注:当
有唯一公共点(注:当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 的交点在y轴两侧).
的交点在y轴两侧).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com