
 如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
如图所示,已知P是?ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.分析 (1)根据BC∥AD,我们可以知道BC∥平面PAD,由于平面PBC∩平面PAD=l,可以证得BC∥l;
(2)取CD的中点Q,连接MQ、NQ,可证平面MNQ∥平面PAD,再由面面平行的性质得线面平行.
解答 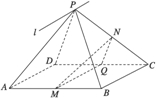 证明:(1)∵BC∥AD,BC?面PAD,∴BC∥面PAD,
证明:(1)∵BC∥AD,BC?面PAD,∴BC∥面PAD,
∵面PBC∩面PAD=l,∴BC∥l.(6分)
(2)取CD的中点Q,连结NQ,MQ,
则NQ∥PD,MQ∥AD,又∵NQ∩MQ=Q,PD∩AD=D,
∴平面MNQ∥平面PAD.又∵MN?平面MNQ,
∴MN∥平面PAD. (12分)
点评 本题以四棱锥为载体,考查线线平行,线面平行,证题的关键是合理运用线面平行的判定及性质定理.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | [-1,0)∪(0,1] | C. | (-∞,1] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
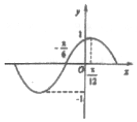 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18,5 | B. | 18,25 | C. | 90,25 | D. | 90,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
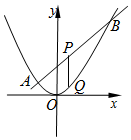 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com