
如图1,在y轴的正半轴上依次有点A1,A2,…,An,…,A1,A2的坐标分别为(0,1),(0,10),且 (n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且
(n=2,3,4,…). 在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…,点B1的坐标为(3,3),且 (n=2,3,4,…).
(n=2,3,4,…).
(1)用含n的式子表示 ;
;
(2)用含n 的式子分别表示点An、Bn的坐标;
(3)求四边形 面积的最大值.
面积的最大值.

(1)∴ 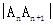 =
=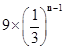
(2)∴点An的坐标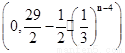 ,∴Bn的坐标为(2n+1,2n+1)
,∴Bn的坐标为(2n+1,2n+1)
3)∴ Sn的最大值为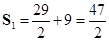 .
.
【解析】(1)由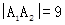 ,
,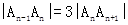 (n=2,3,4,…), 知
(n=2,3,4,…), 知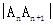 (n=2,3,4,…),组成以9为首项,3为公比的等比数列,所以
(n=2,3,4,…),组成以9为首项,3为公比的等比数列,所以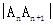 =
=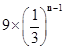 ;
;
(2)因为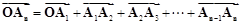 ,由(1)和在y轴的正半轴上依次有点A1,A2,…,An,…,得
,由(1)和在y轴的正半轴上依次有点A1,A2,…,An,…,得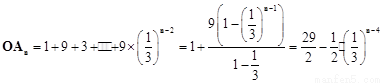 ,
,
即点An的坐标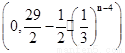 ;由
;由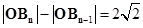 ,
,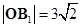
得{|OBn|}是以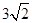 为首项,
为首项,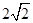 为公差的等差数列;利用等差数列的通项公式得
为公差的等差数列;利用等差数列的通项公式得
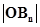 ,即得Bn的坐标;(3)把四边形
,即得Bn的坐标;(3)把四边形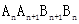 面积分成两个三角形的面积的差,根据三角形的面积公式和(2)可求得,研究数列的单调性得到最大值.
面积分成两个三角形的面积的差,根据三角形的面积公式和(2)可求得,研究数列的单调性得到最大值.
(1)∵ ,
,
∴ 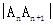 =
=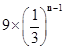 ……………………………………4分
……………………………………4分
(2)由(1)得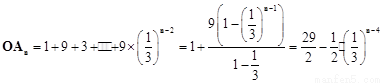
∴点An的坐标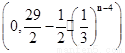 ,
……………………………………6分
,
……………………………………6分
∵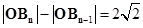 ,
,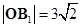
∵{|OBn|}是以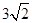 为首项,
为首项,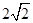 为公差的等差数列
为公差的等差数列
∴ 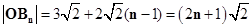
∴Bn的坐标为(2n+1,2n+1) ……………………………………10分
(3)连接An+1Bn+1,设四边形AnAn+1Bn+1Bn的面积为Sn,
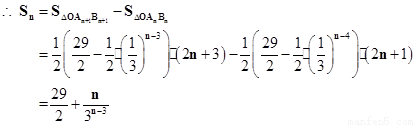
∴ 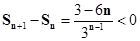 ,即Sn+1<Sn,
,即Sn+1<Sn,
∴ {Sn} 单调递减数列
∴ Sn的最大值为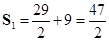 .
.


科目:高中数学 来源: 题型:
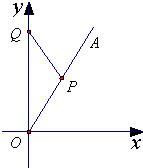 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为2| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
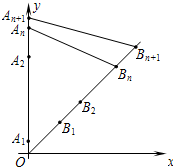 如图,在y轴的正半轴上依次有点A1、A2、…An…,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4…),在射线y=x(x≥0)上依次有点B1、B2…、Bn…,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1、A2、…An…,其中点A1(0,1)、A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4…),在射线y=x(x≥0)上依次有点B1、B2…、Bn…,点B1的坐标为(3,3),且|OBn|=|OBn-1|+2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
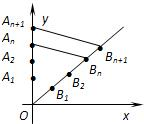 如图,在y轴的正半轴上依次有点A1,A2,…,An,…其中点A1(0,1),A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…点B1的坐标为(3,3),且|OBn|=|OBn-1|+2
如图,在y轴的正半轴上依次有点A1,A2,…,An,…其中点A1(0,1),A2(0,10),且|An-1An|=3|AnAn+1|(n=2,3,4,…),在射线y=x(x≥0)上依次有点B1,B2,…,Bn,…点B1的坐标为(3,3),且|OBn|=|OBn-1|+2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
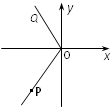 如图,角α 的顶点在直角坐标原点、始边在y轴的正半轴、终边经过点P(-3,-4).角β 的顶点在直角坐标原点、始边在x 轴的正半轴,终边OQ落在第二象限,且tanβ=-2.
如图,角α 的顶点在直角坐标原点、始边在y轴的正半轴、终边经过点P(-3,-4).角β 的顶点在直角坐标原点、始边在x 轴的正半轴,终边OQ落在第二象限,且tanβ=-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com