
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点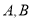 所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;
(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.

(1)6,(2)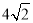 .
.
【解析】
试题分析:(1)由题意得:保持其缺口宽度不变,需在A,B点处分别作抛物线的切线. 以抛物线顶点为原点,对称轴为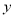 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则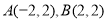 ,从而边界曲线的方程为
,从而边界曲线的方程为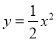 ,
,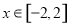 .因为抛物线在点
.因为抛物线在点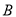 处的切线斜率
处的切线斜率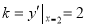 ,所以,切线方程为
,所以,切线方程为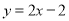 ,与
,与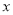 轴的交点为
轴的交点为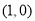 .此时梯形的面积
.此时梯形的面积 平方分米,即为所求.(2)若保持其缺口深度不变,需使两腰分别为抛物线的切线. 设梯形腰所在直线与抛物线切于
平方分米,即为所求.(2)若保持其缺口深度不变,需使两腰分别为抛物线的切线. 设梯形腰所在直线与抛物线切于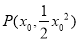 时面积最小.此时,切线方程为
时面积最小.此时,切线方程为 ,其与直线
,其与直线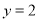 相交于
相交于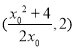 ,与
,与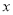 轴相交于
轴相交于 .此时,梯形的面积
.此时,梯形的面积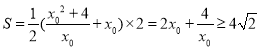 ,
,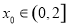 .故,当
.故,当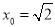 时,面积有最小值为
时,面积有最小值为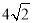 .
.
【解析】
(1)以抛物线顶点为原点,对称轴为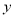 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则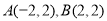 ,
,
从而边界曲线的方程为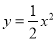 ,
,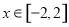 .
.
因为抛物线在点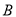 处的切线斜率
处的切线斜率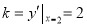 ,
,
所以,切线方程为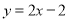 ,与
,与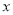 轴的交点为
轴的交点为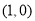 .
.
此时梯形的面积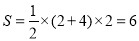 平方分米,即为所求.
平方分米,即为所求.
(2)设梯形腰所在直线与抛物线切于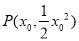 时面积最小.
时面积最小.
此时,切线方程为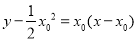 ,
,
其与直线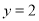 相交于
相交于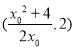 ,
,
与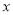 轴相交于
轴相交于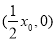 .
.
此时,梯形的面积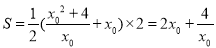 ,
,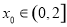 .……11分
.……11分
(这儿也可以用基本不等式,但是必须交代等号成立的条件)
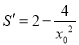 =0,得
=0,得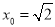 ,
,
当 时,
时,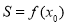 单调递减;
单调递减;
当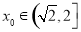 时,
时,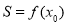 单调递增,
单调递增,
故,当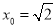 时,面积有最小值为
时,面积有最小值为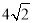 .
.
考点:利用导数研究函数最值


科目:高中数学 来源:2013-2014学年江苏省淮安市高三5月信息卷文科数学试卷(解析版) 题型:填空题
在平面直角坐标系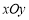 中,抛物线
中,抛物线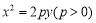 上纵坐标为2的一点到焦点的距离为3,则抛物线的焦点坐标为 .
上纵坐标为2的一点到焦点的距离为3,则抛物线的焦点坐标为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省淮安市高三Ⅲ级部决战四统测二文科数学试卷(解析版) 题型:填空题
某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20 种,从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练理科数学试卷(解析版) 题型:解答题
如图所示的几何体中,面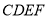 为正方形,面
为正方形,面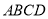 为等腰梯形,
为等腰梯形, 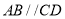 ,
,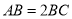 ,
,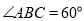 ,且平面
,且平面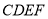
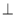 平面
平面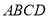 .
.
(1)求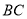 与平面
与平面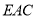 所成角的正弦值;
所成角的正弦值;
(2)线段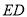 上是否存在点
上是否存在点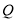 ,使平面
,使平面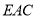
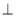 平面
平面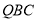 ?
?
证明你的结论.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练文科数学试卷(解析版) 题型:填空题
将函数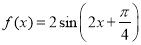 的图像向右平移
的图像向右平移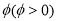 个单位,再将图像上每一点横坐标缩短到原来的
个单位,再将图像上每一点横坐标缩短到原来的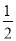 倍,所得图像关于直线
倍,所得图像关于直线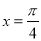 对称,则
对称,则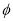 的最小正值为 .
的最小正值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com