
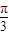 个单位,得到函数y=sin(2x-
个单位,得到函数y=sin(2x-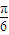 )的图象.
)的图象.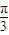 ,得到的函数为
,得到的函数为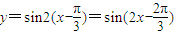 即可判断
即可判断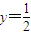 和
和 ,两直线垂直所以正确;
,两直线垂直所以正确;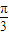 ,得到的函数为
,得到的函数为 ,所以不正确.
,所以不正确.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2011届四川省成都外国语学校高三下学期3月月考数学理卷 题型:填空题
.下面给出的四个命题中:
①对任意的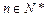 ,点
,点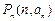 都在直线
都在直线 上是数列
上是数列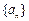 为等差数列的充分不必要条件;
为等差数列的充分不必要条件;
②“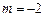 ”是直线
”是直线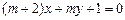 与“直线
与“直线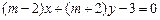 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆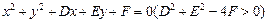 与坐标轴有4个交点
与坐标轴有4个交点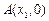 ,
,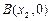 ,
,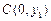 ,
,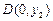 ,则有
,则有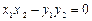 ;
;
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高三下学期3月月考数学理卷 题型:填空题
.下面给出的四个命题中:
①对任意的 ,点
,点 都在直线
都在直线 上是数列
上是数列 为等差数列的充分不必要条件;
为等差数列的充分不必要条件;
②“ ”是直线
”是直线 与“直线
与“直线 相互垂直”的必要不充分条件;
相互垂直”的必要不充分条件;
③设圆 与坐标轴有4个交点
与坐标轴有4个交点 ,
, ,
, ,
,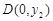 ,则有
,则有 ;
;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com