
 的概率是多少?
的概率是多少? 的长度,再将求得的长度值与整个绳子长度求比值即得.
的长度,再将求得的长度值与整个绳子长度求比值即得. 解:(1)若想两段长短都大于
解:(1)若想两段长短都大于 ,则只能在两个三等分点之间剪断,则其概率为
,则只能在两个三等分点之间剪断,则其概率为 .
.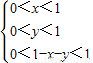 ⇒
⇒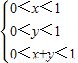 其区域构成三角形OAB(如图14-4-5).
其区域构成三角形OAB(如图14-4-5). ⇒
⇒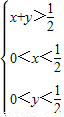 此时的区域为三角形CDE,故所求概率为
此时的区域为三角形CDE,故所求概率为 .
.

 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
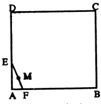 有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )
有一条长度为1的线段EF,其端点E、F在边长为3的正方形ABCD的四边滑动,当F绕着正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )| A、8 | B、11 | C、12 | D、10 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年内蒙古高三下学期综合检测(一)理科数学试卷(解析版) 题型:选择题
如图,有一条长度为1的线段EF,其端点E、F分别在边长为3的正方形ABCD的四边上滑动,当F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹长度最接近于( )

A.8 B.11
C.12 D.10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com