
【题目】已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(Ⅰ)若用数组![]() 中的
中的![]() 分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组
分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组![]() 的所有情形,并回答一共有多少种;
的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
【答案】(1)(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种
(2)猜4或5获奖的可能性最大
【解析】
第一问中,先分析所有的情况为共有8种,
第二问,由于事件![]() 包含1个基本事件,事件
包含1个基本事件,事件![]() 包含3个基本事件,事件
包含3个基本事件,事件![]() 包含3个基本事件,事件
包含3个基本事件,事件![]() 包含1个基本事件,然后利用古典概型的概率计算公式得到,比较大小即可.
包含1个基本事件,然后利用古典概型的概率计算公式得到,比较大小即可.
解:(Ⅰ)数组![]() 的所有情形为:(1,1,1),(1,1,2),(1,2,1),
的所有情形为:(1,1,1),(1,1,2),(1,2,1),
(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2),共8种.
答:一共有8种. ………………………5分
注:列出5、6、7种情形,得2分;列出所有情形,得4分;写出所有情形共8种,得1分.
(Ⅱ)记“所摸出的三个球号码之和为![]() ”为事件
”为事件![]() (
(![]() =3,4,5,6), ………6分
=3,4,5,6), ………6分
易知,事件![]() 包含1个基本事件,事件
包含1个基本事件,事件![]() 包含3个基本事件,事件
包含3个基本事件,事件![]() 包含3个基本事件,事件
包含3个基本事件,事件![]() 包含1个基本事件,所以,
包含1个基本事件,所以,
![]() ,
,![]() ,
,![]() ,
,![]() . ……………………10分
. ……………………10分
故所摸出的两球号码之和为4、为5的概率相等且最大.
答:猜4或5获奖的可能性最大. ……………………12分


科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若p∨q为真命题,则p∧q为真命题
B.“x=5”是“x2-4x-5=0”的充分不必要条件
C.命题“若x<-1,则x2-2x-3>0”的否定为:“若x≥-1,则x2-2x-3≤0”
D.已知命题p:x∈R,x2+x-1<0,则![]() p:x∈R,x2+x-1≥0
p:x∈R,x2+x-1≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)
等边△ABC的边长为3,点D,E分别为AB,AC上的点,且满足![]() (如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
(如图①),将△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,连接A1B,A1C(如图②).
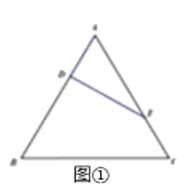
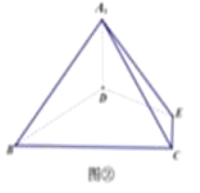
(1)求证:A1D⊥平面BCED;
(2)在线段BC上是否存在点P(不包括端点),使直线PA1与平面A1BD所成的角为60°?若存在,求出A1P的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于两点
交于两点![]() ,点
,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 在
在![]() 的单调区间;
的单调区间;
(Ⅱ)方程![]() 有3个不同的实根,求实数
有3个不同的实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,已知椭圆的长轴为
的左、右焦点,已知椭圆的长轴为![]() 是椭圆
是椭圆![]() 上一动点,
上一动点,![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为椭圆
为椭圆![]() 上一点,
上一点,![]() 为坐标原点,且满足
为坐标原点,且满足![]() ,其中
,其中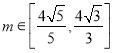 ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex,g(x)=a(lnx+x).
(1)当a=e时,求证:f(x)≥g(x)恒成立;
(2)当a>0时,求证:f(x)≤g(x)+1恒有解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,2],log2(x+2)<2m;命题q:关于x的方程x2﹣x+m2=0有两个不同的实数根.
(1)若(¬p)∧q为真命题,求实数m的取值范围;
(2)若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com