
(本题满分14分) 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=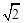 ,AD=3,BB1=1.
,AD=3,BB1=1.
(Ⅰ) 设O是线段BD的中点,
求证:C1O∥平面AB1D1;
(Ⅱ) 求直线AB1与平面ADD1所成的角.
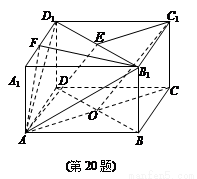
(Ⅰ)略
(Ⅰ) 45°.
【解析】
(Ⅰ) 证明:取B1D1的中点E,连结C1E,OA,则A,O,C共线,且 C1E=OA,
因为BCD-B1C1D1为三棱柱,
所以平面BCD∥平面B1C1D1,
故C1E∥OA,
所以C1EAO为平行四边形,
从而C1O∥EA.[来源:Z&xx&k.Com]
又因为C1O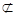 平面AB1D1,
平面AB1D1,
EA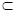 平面AB1D1,
平面AB1D1,
所以C1O∥平面AB1D1.………………………………………………7分
(Ⅱ) 解:过B1在平面B1C1D1内作B1A1∥C1D1,使B1A1=C1D1.
连结A1D1,AA1.
过B1作A1D1的垂线,垂足为F,
则B1F⊥平面ADD1,
所以∠B1AF为AB1与平面ADD1所成的角.
在Rt△A1B1F中,B1F=A1B1 sin 60°=
sin 60°= .
.
在Rt△AB1F中,AB1= ,
,
故sin∠B1AF =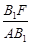 =
= .
.
所以∠B1AF=45°.
即直线AB1与平面ADD1所成角的大小为45°. …………………14分


科目:高中数学 来源: 题型:
(本题满分14分)
如图,在四棱锥![]() 中,底面
中,底面![]() ABCD是正方形,侧棱
ABCD是正方形,侧棱![]() 底面ABCD,
底面ABCD,![]() ,E是PC的中点,作
,E是PC的中点,作![]() 交PB于点F。
交PB于点F。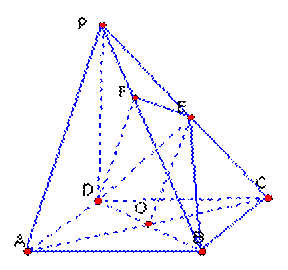
(I)证明 ![]() 平面
平面![]() ;
;
(II)证明![]() 平面EFD;
平面EFD;
(III)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:包头33中09-10高二下学期期中理科数学试题 题型:解答题
(本题满分14分)
如图,在四棱锥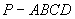 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱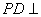 底面ABCD,
底面ABCD,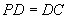 ,E是PC的中点,作
,E是PC的中点,作 交PB于点F。
交PB于点F。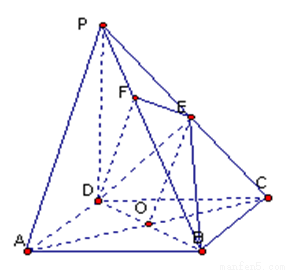
(I)证明 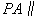 平面
平面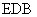 ;
;
(II)证明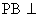 平面EFD;
平面EFD;
(III)求二面角 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三第一次教学质量检测一级达标校数学理卷 题型:解答题
(本题满分14分)
已知函数 .
.
(Ⅰ)若 为
为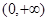 上的单调函数,试确定实数
上的单调函数,试确定实数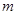 的取值范围;
的取值范围;
(Ⅱ)求函数 在定义域上的极值;
在定义域上的极值;
(Ⅲ)设 ,求证:
,求证: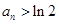 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(非一级校) 题型:解答题
.(本题满分14分)
设函数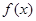 =
=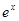 (
(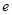 为自然对数的底数),
为自然对数的底数),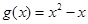 ,记
,记 .
.
(Ⅰ)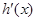 为
为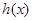 的导函数,判断函数
的导函数,判断函数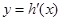 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)若函数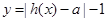 =0有两个零点,求实数
=0有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三下学期期中考试理数 题型:解答题
(本题满分14分)
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l: .
.
⑴ 求椭圆的标准方程;
⑵ 设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com