
分析 根据所给函数f(x)=$\frac{x}{3x+1}$,及数列{an}满足a1=1,an+1=f(an)(n∈N*)即可获得{an}的递推关系,然后通过推出 $\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2得到证明.
解答 证明:由已知得,an+1=f(an)可得an+1=$\frac{{a}_{n}}{{2a}_{n}+1}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+2,即 $\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=2.a1=1,∴$\frac{1}{{a}_{1}}=1$,
∴数列{$\frac{1}{{a}_{n}}$}是首项为1,公差d=2的等差数列.
点评 本题考查等差数列的判定,揭示了函数和数列的内在联系,数列递推关系式的应用,考查计算能力.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
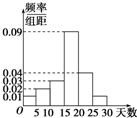
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com