
【题目】下面四个命题:其中所有正确命题的序号是_________.
①函数![]() 的最小正周期为
的最小正周期为![]() ;
;
②在![]() 中,若
中,若![]() ,则
,则![]() 一定是钝角三角形;
一定是钝角三角形;
③函数![]() 且
且![]() 的图象必经过点(3,2);
的图象必经过点(3,2);
④若命题“![]() ”是假命题,则实数
”是假命题,则实数![]() 的取值范围为
的取值范围为![]() ;
;
⑤![]() 的图象向左平移
的图象向左平移![]() 个单位,所得图象关于
个单位,所得图象关于![]() 轴对称.
轴对称.
【答案】②③④
【解析】
①:根据周期的定义,结合正弦的诱导公式进行判断即可;
②:根据平面向量数量积的定义,结合三角形内角的取值范围进行判断即可;
③:根据对数的运算性质进行判断即可;
④:根据命题的否定与原命题的真假关系进行判断即可;
⑤:先利用辅助角公式把函数的解析式化简成余弦型函数解析式的形式,根据平移规律求出平行后的解析式,再判断是否是偶函数进行判断即可.
①:当![]() 时,
时,![]() ,
,![]() ,所以函数
,所以函数![]() 的最小正周期为
的最小正周期为![]() 是错误的,故本命题是假命题;
是错误的,故本命题是假命题;
②:![]()
![]() ,因此
,因此![]() 一定是钝角三角形,故本命题是真命题;
一定是钝角三角形,故本命题是真命题;
③:因为当![]() 时,
时,![]() ,所以函数
,所以函数![]() 且
且![]() 的图象必经过点(3,2),故本命题是真命题;
的图象必经过点(3,2),故本命题是真命题;
④:命题“![]() ”是假命题,因此它的否定是真命题,即
”是假命题,因此它的否定是真命题,即
![]() 是真命题,因此要想该命题是真命题,只需
是真命题,因此要想该命题是真命题,只需![]() ,故本命题是真命题;
,故本命题是真命题;
⑤:![]() ,该函数的图象向左平移
,该函数的图象向左平移![]() 个单位后,得到函数
个单位后,得到函数![]() ,而
,而![]() 是奇函数关于原点对称,不关于关于
是奇函数关于原点对称,不关于关于![]() 轴对称,故本命题是假命题.
轴对称,故本命题是假命题.
故答案为:②③④


科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于圆锥曲线的命题中:
①双曲线![]() 与椭圆
与椭圆![]() 有相同焦点;
有相同焦点;
②以抛物线的焦点弦(过焦点的直线截抛物线所得的线段)为直径的圆与抛物线的准线是相切的;
③设![]() 、
、![]() 为两个定点,
为两个定点,![]() 为常数,若
为常数,若![]() ,则动点
,则动点![]() 的轨迹为双曲线;
的轨迹为双曲线;
④过抛物线![]() 的焦点作直线与抛物线相交于
的焦点作直线与抛物线相交于![]() 、
、![]() ,则使它们的横坐标之和等于5的直线有且只有两条;
,则使它们的横坐标之和等于5的直线有且只有两条;
以上命题正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
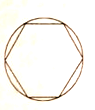
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)
A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中不正确的个数是( )
①若直线![]() 上有无数个点不在平面
上有无数个点不在平面![]() 内,则
内,则![]() ;
;
②和两条异面直线都相交的两条直线异面;
③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;
④一条直线和两条异面直线都相交,则它们可以确定两个平面.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的对称轴上一点
的对称轴上一点![]() 的直线与抛物线相交于M、N两点,自M、N向直线
的直线与抛物线相交于M、N两点,自M、N向直线![]() 作垂线,垂足分别为
作垂线,垂足分别为![]() 、
、![]() .
.
(Ⅰ)当![]() 时,求证:
时,求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)记![]()
![]() 、
、![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,是否存在
,是否存在![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]() 成立.若存在,求
成立.若存在,求![]() 值;若不在,说明理由.
值;若不在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com