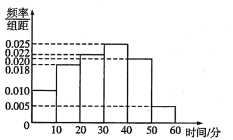
【题目】某公司为了了解某地区电视观众对某类体育节目的收视情况随机抽取了100名观众进行调查，其中女性有55名.如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图.将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.
（1）根据已知条件完成下面的
列联表，并据此资料你是否认为“体育迷”与性别有关？
（2）将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.
【答案】（1）详见解析（2）
【解析】
试题分析：（1）根据所给的频率分布直方图得出数据列出列联表，再代入公式计算得出K方，与3.841比较即可得出结论；（2）由题意，列出所有的基本事件，计算出事件“任选3人，至少有1人是女性”包含的基本事件数，即可计算出概率
试题解析：（1）由频率分布直方图可知，在抽取的100人中，“体育迷”有25人，从而完成2×2列联表如下：
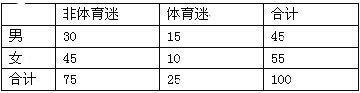
将2×2列联表中的数据代入公式计算，得
因为
，所以我们没有理由认为“体育迷”与性别有关.
（2）由频率分布直方图可知，“超级体育迷”有5人，从而一切可能结果所组成的基本事件空间为
.
其中
表示男性，
.
表示女性，
由10个基本事件组成，而且这些基本事件的出现是等可能的.
用
表示“任选2人中，至少有1人是女性”这一事件，则
.
事件
由7个基本事件组成，因而
.
科目：高中数学 来源： 题型：
【题目】2018年6月14日，第二十一届世界杯足球赛将在俄罗斯拉开帷幕.为了了解喜爱足球运动是否与性别有关，某体育台随机抽取100名观众进行统计，得到如下
列联表.
（1）将列联表补充完整，并判断能否在犯错误的概率不超过0.001的前提下认为喜爱足球运动与性别有关？
（2）在不喜爱足球运动的观众中，按性别分别用分层抽样的方式抽取6人，再从这6人中随机抽取2人参加一台访谈节目，求这2人至少有一位男性的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】用红、黄、蓝、白、黑五种颜色涂在如图所示的四个区域内，每个区域涂一种颜色，相邻两个区域涂不同的颜色，五种颜色可以反复使用，共有___________种不同的涂色方法？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）=x2﹣a|x﹣1|+b（a＞0，b＞﹣1）
（1）若b=0，a＞2，求f（x）在区间[0，2]内的最小值m（a）；
（2）若f（x）在区间[0，2]内不同的零点恰有两个，且落在区间[0，1），（1，2]内各一个，求a﹣b的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国古代数学著作《九章算术》中有如下问题：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升.问：米几何？”如图所示的是解决该问题的程序框图，执行该程序框图，若输出的
（单位：升），则输入
的值为（ ）
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义函数F（a，b）= 
（a+b﹣|a﹣b|）（a，b∈R），设函数f（x）=﹣x2+2x+4，g（x）=x+2（x∈R）函数F（f（x），g（x））的最大值与零点之和为（ ）
A.4
B.6
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}是等差数列，Sn为{an}的前n项和，且a10=19，S10=100；数列{bn}对任意n∈N* ， 总有b1b2b3…bn﹣1bn=an+2成立．
（Ⅰ）求数列{an}和{bn}的通项公式；
（Ⅱ）记cn=（﹣1）n 
，求数列{cn}的前n项和Tn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
