
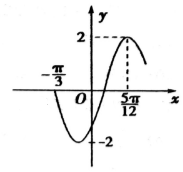
 函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ),x∈R,(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示.分析 (Ⅰ)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数f(x)解析式.
(Ⅱ)利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(Ⅲ)由条件求得故$tan(α-\frac{π}{3})=\frac{5}{12}$,再利用二倍角的正切公式,求得$tan2(α-\frac{π}{3})$的值.
解答 解:(Ⅰ)根据函数f(x)=Asin(ωx+φ)的图象知A=2.
∵$\frac{3T}{4}$=$\frac{5π}{12}$-($\frac{π}{3}$),∴T=π.∴ω=2.
由五点法作图知当x=$\frac{5π}{12}$时,ωx+φ=$\frac{π}{2}$,
即2×$\frac{5}{12}$π+φ=$\frac{π}{2}$,∴φ=-$\frac{π}{3}$.故$f(x)=2sin(2x-\frac{π}{3})$.
(Ⅱ)先把y=sinx的图象向右平移$\frac{π}{3}$个单位长度得到$y=sin(x-\frac{π}{3})$的图象,
使曲线上各点的横坐标变为原来的$\frac{1}{2}$,得到函数$y=sin(2x-\frac{π}{3})$的图象,
最后把曲线上各点的纵坐标变为原来的2倍,得到$y=2sin(2x-\frac{π}{3})$.
(Ⅲ)由$f(\frac{α}{2})=\frac{10}{13}$得$sin(α-\frac{π}{3})=\frac{5}{13}$,因为$\frac{π}{3}<α<\frac{{5{π}}}{6}$
所以$0<α-\frac{π}{3}<\frac{π}{2}$,得$cos(α-\frac{π}{3})=\frac{12}{13}$,故$tan(α-\frac{π}{3})=\frac{5}{12}$,
∴$tan2(α-\frac{π}{3})=\frac{{2tan(α-\frac{π}{3})}}{{1-{{tan}^2}(α-\frac{π}{3})}}=\frac{120}{119}$.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值.函数y=Asin(ωx+φ)的图象变换规律,二倍角的正切公式,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2..
在长方体ABCD-A1B1C1D1中,E,F分别是AB,CD1的中点,AA1=AD=1,AB=2..查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6π}{5}$ | B. | $\frac{5π}{6}$ | C. | $\frac{7π}{6}$ | D. | $\frac{12π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m<1或m>3 | B. | 1<m<3 | C. | m<3 | D. | m>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.
如图,在三棱柱ABC-A1B1C1中,CA=CB=AA1,∠BAA1=∠BAC=60°,点O是线段AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com