
分析 (1)利用甲击中目标的概率是$\frac{3}{4}$;甲,丙同时轰炸一次,目标未被击中的概率是$\frac{1}{12}$;乙、丙同时轰炸一次郡击中目标的概率是$\frac{1}{4}$,且甲,乙,丙是否击中目标相互独立,建立方程,求乙,丙各自击中目标的概率;
(2)X的取值为0,1,2,3,求出相应的概率,可得X的数学期望.
解答 解:(1)记甲、乙、丙各自独立击中目标的事件分别为A、B、C.则
由已知得P(A)=$\frac{3}{4}$,P($\overline{A}\overline{C}$ )=$\frac{1}{4}$[1-P(C)]=$\frac{1}{12}$,∴P(C)=$\frac{2}{3}$
由P(BC)=P(B)P(C)=$\frac{1}{4}$,得$\frac{2}{3}$P(B)=$\frac{1}{4}$,∴P(B)=$\frac{3}{8}$;
(2)X的取值为0,1,2,3,则
P(X=0)=$\frac{1}{4}$×$\frac{1}{3}×\frac{5}{8}$=$\frac{5}{96}$,P(X=1)=$\frac{3}{4}$×$\frac{1}{3}$×$\frac{5}{8}$+$\frac{1}{4}$×$\frac{2}{3}$×$\frac{5}{8}$+$\frac{1}{4}×\frac{1}{3}×\frac{3}{8}$=$\frac{28}{96}$,
P(X=2)=$\frac{1}{4}$×$\frac{2}{3}$×$\frac{3}{8}$+$\frac{3}{4}$×$\frac{2}{3}$×$\frac{5}{8}$+$\frac{3}{4}$×$\frac{1}{3}$×$\frac{3}{8}$=$\frac{45}{96}$,
P(X=3)=$\frac{3}{4}$×$\frac{2}{3}$×$\frac{3}{8}$=$\frac{18}{96}$,
∴EX=0×$\frac{5}{96}$+1×$\frac{28}{96}+2×\frac{45}{96}+3×\frac{18}{96}$=$\frac{43}{24}$.
点评 本题考查概率的计算,考查数学期望,考查学生的计算能力,正确求概率是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
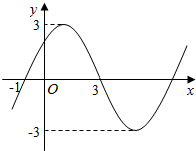 如图,它是函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))图象的一部分,则f(0)的值为$\frac{3\sqrt{2}}{2}$.
如图,它是函数f(x)=Asin(ωx+φ)(A>0,ω>0,φ∈[0,2π))图象的一部分,则f(0)的值为$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
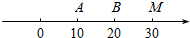 如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y表示C到A的距离4倍与C到距离的6倍的和.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2011 | B. | -2012 | C. | -2013 | D. | -2014 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {2,5} | C. | {2,3,5} | D. | {2,3,5,8} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)g(x)是偶函数 | B. | |f(x)|g(x)是奇函数 | C. | f(-x)是奇函数 | D. | |g(x)|是奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com