
【题目】已知函数![]() ,在点
,在点![]() 处的切线方程为
处的切线方程为![]() ,求(1)实数
,求(1)实数![]() 的值;(2)函数
的值;(2)函数![]() 的单调区间以及在区间
的单调区间以及在区间![]() 上的最值.
上的最值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由题已知点![]() 处的切线方程
处的切线方程![]() ,可获得两个条件;即:点
,可获得两个条件;即:点![]()
再函数的图像上,令点![]() 处的导数为切线斜率。可得两个方程,求出
处的导数为切线斜率。可得两个方程,求出![]() 的值
的值
(2)由(1)已知函数的解析式,可运用导数求出函数的单调区间和最值。即:
![]() 为函数的增区间,反之为减区间。最值需求出极值与区间端点值比较而得。
为函数的增区间,反之为减区间。最值需求出极值与区间端点值比较而得。
试题解析:(1)因为在点![]() 处的切线方程为
处的切线方程为![]() ,所以切线斜率是
,所以切线斜率是![]() ,
,
且![]() ,求得
,求得![]() ,即点
,即点![]() ,
,
又函数![]() ,则
,则![]()
所以依题意得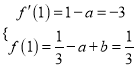 ,解得
,解得![]()
(2)由(1)知![]() ,所以
,所以![]()
令![]() ,解得
,解得![]() ,当
,当![]() ;当
;当![]()
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
又![]() ,所以当x变化时,f(x)和f′(x)变化情况如下表:
,所以当x变化时,f(x)和f′(x)变化情况如下表:
X | 0 | (0,2) | 2 | (2,3) | 3 |
f′(x) | - | 0 | + | 0 | |
f(x) | 4 | ↘ | 极小值 | ↗ | 1 |
所以当![]() 时,
时, ![]() ,
, ![]()


科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在复数范围内解方程![]() (
(![]() 为虚数单位)
为虚数单位)
(2)设![]() 是虚数,
是虚数,![]() 是实数,且
是实数,且![]()
(i)求![]() 的值及
的值及![]() 的实部的取值范围;
的实部的取值范围;
(ii)设![]() ,求证:
,求证:![]() 为纯虚数;
为纯虚数;
(iii)在(ii)的条件下求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的个数是( )
①若直线![]() 平面
平面![]() ,直线
,直线![]() ,则
,则![]() ;②若直线l和平面
;②若直线l和平面![]() 内的无数条直线垂直,则直线l与平面
内的无数条直线垂直,则直线l与平面![]() 必相交;③过平面
必相交;③过平面![]() 外一点有且只有一条直线和平面
外一点有且只有一条直线和平面![]() 垂直;④过直线
垂直;④过直线![]() 外一点有且只有一个平面和直线a垂直
外一点有且只有一个平面和直线a垂直
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日.在平昌冬奥会短道速滑男子500米比赛中.中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况.收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人.已知这20位女生的数据茎叶图如图所示.

(1)将这20位女生的时间数据分成8组,分组区间分别为![]() ,在答题卡上完成频率分布直方图;
,在答题卡上完成频率分布直方图;
(2)以(1)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;
(3)以(1)中的频率估计100位女生中累计观看时间小于20个小时的人数.已知200位男生中累计观看时间小于20小时的男生有50人请完成答题卡中的列联表,并判断是否有99 %的把握认为“该校学生观看冬奥会累计时间与性别有关”.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
附:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的定义域;
的定义域;
(2)若函数![]() 有且仅有一个零点,求实数m的取值范围;
有且仅有一个零点,求实数m的取值范围;
(3)任取![]() ,若不等式
,若不等式![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com