已知椭圆
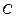
的焦点分别为
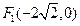
和
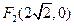
,长轴长为
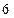
,设直线
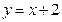
交椭圆
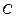
于
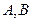
两点,求线段
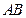
的中点坐标。
线段
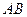
的中点坐标为
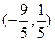
设椭圆
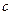
的方程为:
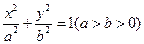
,由题意得:
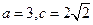
,于是
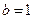
,所以椭圆
的方程为:
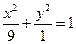
,由
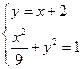
得
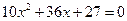
,因为二次方程的差别式
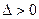
,所以直线与椭圆有两个不同的交点,设
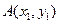
,
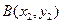
,则
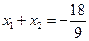
,
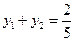
,故线段
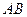
的中点坐标为
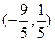
。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
椭圆
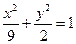
的焦点为
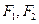
,点
P在椭圆上,若
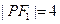
,则

;
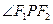
的大小为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知椭圆的长轴是短轴的
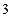
倍,且过点
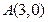
,并且以坐标轴为对称轴,
求椭圆的标准方程。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
椭圆
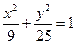
的焦点为
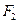
、
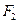
,
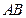
是椭圆过焦点
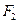
的弦,则
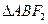
的周长是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
给定四条曲线:①
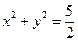
;②
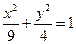
;③
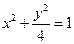
;④
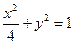
。其中与直线

仅有一个交点的直线是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
焦点在坐标轴上,且
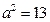
,
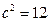
的椭圆的标准方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
过点
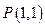
作直线
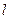
,使得它被椭圆
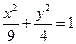
所截出的弦的中点恰为
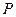
,则直线
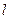
的方程为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
若椭圆的中心在原点,对称轴在坐标轴上,且离心率为
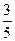
,一条准线的方程为
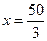
,求椭圆的标准方程。
查看答案和解析>>

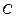 的焦点分别为
的焦点分别为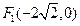 和
和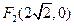 ,长轴长为
,长轴长为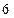 ,设直线
,设直线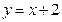 交椭圆
交椭圆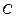 于
于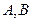 两点,求线段
两点,求线段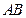 的中点坐标。
的中点坐标。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案