
设三组实验数据(x1,y1),(x2,y2),(x3,y3)的回归直线方程是: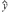 =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
=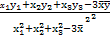 (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),
若有7组数据列表如下:
| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
 xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.  黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y/分 | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢 | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
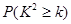 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
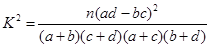 ,其中
,其中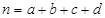 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学高三年级从甲、乙两个班级各选出七名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.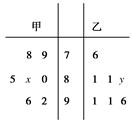
(1)求x和y的值;
(2)计算甲班七名学生成绩的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3000名初中生、4000名高中生中作问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
(3)为了从4000份高中生的答卷中抽取一个容量为64的样本,如何使用系统抽样抽取到所需的样本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.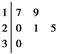
(1)根据茎叶图计算样本均值.
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
空气质量指数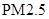 (单位:
(单位: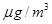 )表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
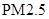 日均浓度 日均浓度 |  | 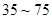 | 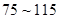 | 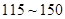 | 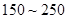 | 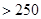 |
| 空气质量级别 | 一级 | 二级 | 三级 | 四级 | 五级 | 六级 |
| 空气质量类别 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
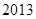 年
年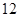 月
月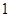 日—
日—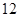 月
月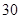 日(
日(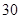 天)对空气质量指数
天)对空气质量指数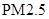 进行监测,获得数据后得到如下条形图.
进行监测,获得数据后得到如下条形图. 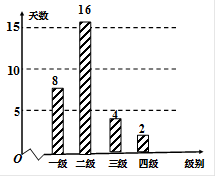
 个,求恰好有一天空气质量类别为中度污染的概率.
个,求恰好有一天空气质量类别为中度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5(PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称可入肺颗粒物)年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
| 组别 | PM2.5(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,15] | 4 | 0.1 |
| 第二组 | (15,30] | 12 | 0.3 |
| 第三组 | (30,45] | 8 | 0.2 |
| 第四组 | (45,60] | 8 | 0.2 |
| 第五组 | (60,75] | 4 | 0.1 |
| 第六组 | (75,90) | 4 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校餐厅新推出A,B,C,D四款套餐,某一天四款套餐销售情况的条形图如下. 为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
| | 满意 | 一般 | 不满意 |
| A套餐 | 50% | 25% | 25% |
| B套餐 | 80% | 0 | 20% |
| C套餐 | 50% | 50% | 0 |
| D套餐 | 40% | 20% | 40% |
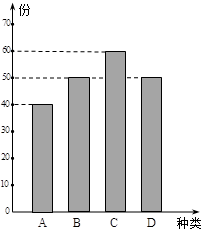
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com