
【题目】商品在近30天内每件的销售价格P(元)与时间t(天)的函数关系p= ![]()
该商品的日销售量Q(件)时间t(天)的函数关系Q=﹣t+40(0<t≤30,t∈N*)
求该商品的日销售额的最大值,并指出日销售额最大一天是30天中的第几天?
【答案】解:当0<t<25,t∈N+时,y=(t+20)(﹣t+40)=﹣t2+20t+800=﹣(t﹣10)2+900.
∴t=10(天)时,ymax=900(元),
当25≤t≤30,t∈N+时,y=(﹣t+100)(﹣t+40)=t2﹣140t+4000=(t﹣70)2﹣900,
而y=(t﹣70)2﹣900,在t∈[25,30]时,函数递减.
∴t=25(天)时,ymax=1125(元).
∵1125>900,∴ymax=1125(元).
故所求日销售金额的最大值为1125元,且在最近30天中的第25天日销售额最大
【解析】根据分段函数不同段上的表达式,分别求最大值最终取较大者分析即可获得问题解答.


科目:高中数学 来源: 题型:
【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是![]() 和
和![]() ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数f(x)= ![]() 是奇函数,其中a,b为实数
是奇函数,其中a,b为实数
(1)求a,b的值
(2)用定义证明f(x)在R上是减函数
(3)若对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点. 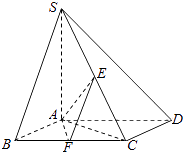
(1)证明:SD⊥AF;
(2)若AB=2,SA=4,求二面角F﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的个数是( )
①命题“所有的四边形都是矩形”是特称命题;
②命题“x∈R,x2+2<0”是全称命题;
③若p:x∈R,x2+4x+4≤0,则q:x∈R,x2+4x+4≤0是全称命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx,g(x)=x2 . 其中x∈R.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)﹣1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)﹣g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为kAB , 若|kAB|≥1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)既是奇函数,又是周期为3的周期函数,当x∈(0, ![]() )时,f(x)=sinπx,f(
)时,f(x)=sinπx,f( ![]() )=0,则函数f(x)在区间[0,6]上的零点个数是( )
)=0,则函数f(x)在区间[0,6]上的零点个数是( )
A.9
B.7
C.5
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com