Question

直线x=1被圆x²+y²+4y=0截得的弦AB的长|AB|=    ．

Answer 1

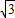
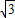
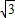
【答案】分析：把直线x=1代入 圆x²+y²+4y=0可解得 A（1，-2- ），B（1，-2+ ），故|AB|=|（-2+ ）-（-2- ）|．
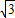
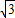
解答：解：把直线x=1代入 圆x²+y²+4y=0可得  y=-2-，或 y=-2+，
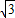
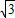
∴A（1，-2- ），B（1，-2+ ）．
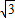
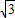
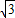
故直线x=1被圆x²+y²+4y=0截得的弦AB的长|AB|=|（-2+ ）-（-2- ）|=2，
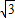
故答案为 2．
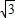
点评：本题考查直线和圆的位置关系，直线被圆截得的弦长，求出弦AB的端点A，B 的坐标是解题的关键．