
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,函数![]() (其中
(其中![]() 为函数
为函数![]() 的导数)的图像关于直线
的导数)的图像关于直线![]() 对称,求函数
对称,求函数![]() 单调区间;
单调区间;
(Ⅲ)在(Ⅱ)的条件下,若对任意的![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)函数
;(Ⅱ)函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减;(Ⅲ)
上单调递减;(Ⅲ) ![]() .
.
【解析】
试题分析:(Ⅰ)由![]() ,得
,得![]() ;(Ⅱ)
;(Ⅱ)![]() 的图象关于直线
的图象关于直线![]() 对称,故函数
对称,故函数![]() 为偶函数,解得
为偶函数,解得![]() ,分别令
,分别令![]() ,
,![]() 即可得到单调区间;(Ⅲ)对任意的
即可得到单调区间;(Ⅲ)对任意的![]() ,都有
,都有![]() 恒成立可转化为
恒成立可转化为![]() 在
在![]() 上恒成立,易知
上恒成立,易知![]() ,∴
,∴![]() 在
在![]() 上恒成立,构造函数
上恒成立,构造函数![]() ,只需
,只需![]() 即可.
即可.
试题解析:(Ⅰ)由![]() 有
有![]()
因为![]() 在
在![]() 处取得极值,故
处取得极值,故![]()
∴![]()
经检验:当![]() 时,符合题意,故
时,符合题意,故![]() .
.
(Ⅱ)由(Ⅰ)知:![]()
∵![]() 的图像关于直线
的图像关于直线![]() 对称,故函数
对称,故函数![]() 为偶函数
为偶函数
又![]()
![]()
∴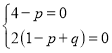 ,解得
,解得![]()
∴![]()
∴![]()
令![]() 有
有![]() 或
或![]()
令![]() 有
有![]() 或
或![]()
∴函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
在区间![]() 上单调递减.
上单调递减.
(Ⅲ)由(Ⅱ)知,对任意的![]() ,都有
,都有![]() 恒成立可转化为
恒成立可转化为
![]() 在
在![]() 上恒成立
上恒成立
易知![]() ∴
∴![]() 在
在![]() 上恒成立
上恒成立
令![]() ,∴
,∴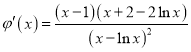
令![]() ,∴
,∴![]()
∴![]() 在
在![]() 上递减,
上递减,![]() 上递增
上递增
∴![]()
∴![]() ,即
,即![]() 在
在![]() 上递增
上递增
∴![]()
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于
轴负半轴于![]() 点,且
点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若过![]() 、
、![]() 、
、![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(3)过![]() 的直线
的直线![]() 与(2)中椭圆交于不同的两点
与(2)中椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
B. 在线性回归分析中,回归直线不一定过样本点的中心![]()
C. 在回归分析中, ![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
D. 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
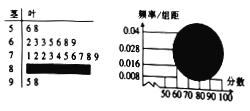
【题目】如图,某校高一(1)班全体男生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分,据此解答如下问题:
(1)求该班全体男生的人数及分数在![]() 之间的男生人数;
之间的男生人数;
(2)根据频率分布直方图,估计该班全体男生的数学平均成绩(同一组中的数据用该组区间的中点值代表);
(3)从分数在![]() 中抽取两个男生,求抽取的两男生分别来自
中抽取两个男生,求抽取的两男生分别来自![]() 、
、![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
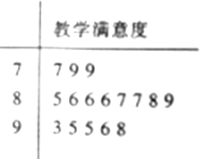
【题目】某学校用“10分制”调查本校学生对教师教学的满意度,现从学生中随机抽取16名,以下茎叶图记录了他们对该校教师教学满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(Ⅰ)若教学满意度不低于9.5分,则称该生对教师的教学满意度为“极满意”.求从这16人中随机选取3人,至少有1人是“极满意”的概率;
(Ⅱ)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记![]() 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经测算,某型号汽车在匀速行驶过程中每小时耗油量![]() (升)与速度
(升)与速度![]() (千米/每小时)
(千米/每小时) ![]() 的关系可近似表示为:
的关系可近似表示为: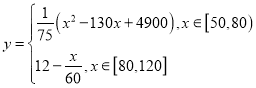 .
.
(Ⅰ)该型号汽车速度为多少时,可使得每小时耗油量最低?
(Ⅱ)已知![]() 两地相距120公里,假定该型号汽车匀速从
两地相距120公里,假定该型号汽车匀速从![]() 地驶向
地驶向![]() 地,则汽车速度为多少时总耗油量最少?
地,则汽车速度为多少时总耗油量最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为
,离心率为![]() ,以椭圆
,以椭圆![]() 的端州的两端点和两焦点所围成的四边形的周长为8,直线
的端州的两端点和两焦点所围成的四边形的周长为8,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程
的方程![]() 为抛物线
为抛物线![]() 上一点,
上一点,![]() 为抛物线的焦点.
为抛物线的焦点.
(I)求![]() ;
;
(II)设直线![]() 与抛物线
与抛物线![]() 有唯一公共点
有唯一公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com