已知函数f(x)=x2-2x,g(x)=ax+2,其中a>0.
(Ⅰ)对?x∈[-1,2],有f(x)<g(x)+2成立,求正数a的取值范围.
(Ⅱ)对?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),求正数a的取值范围.
解:(I)由题意,h(x)=f(x)-g(x)-2=x
2-(2+a)x-4<0对任意x∈[-1,2]恒成立,
只需
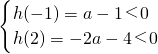
成立,故0<a<1.
(II)当a>0时,g(x)=ax+2在[-1,2]上的值域A=[2-a,2+2a],
f(x)=x
2-2x在[-1,2]上的值域B=[-1,3],
由题意,A⊆B,得
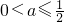
.
分析:(I)根据对?x∈[-1,2],有f(x)<g(x)+2成立,即h(x)=f(x)-g(x)-2=x
2-(2+a)x-4<0对任意x∈[-1,2]恒成立,只需
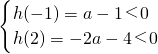
成立,解此不等式组即可求得正数a的取值范围;
(Ⅱ)先求出两个函数在[-1,2]上的值域分别为A、B,再根据对任意的x
1∈[-1,2],存在x
0∈[-1,2],使g(x
1)=f(x
0),集合A是集合B的子集,并列出不等式,解此不等式组即可求得实数a的取值范围,注意条件a>0.
点评:此题是个中档题.考查函数的值域,难点是题意的理解与转化,体现了转化的思想.同时也考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

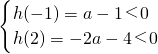 成立,故0<a<1.
成立,故0<a<1.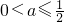 .
.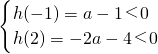 成立,解此不等式组即可求得正数a的取值范围;
成立,解此不等式组即可求得正数a的取值范围;

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<