
����Ŀ��һ��������װ��������ŷֱ�Ϊ1��2��3�ĺ����������ŷֱ�Ϊ1��2��3�İ��������������ŷֱ��Ϊa1 �� a2 �� a3 �� �����������ŷֱ��Ϊb1 �� b2 �� b3 �� ���е�6�������ɫ�ͱ����û���κβ��죬�ִӴ���һ�������ȡ��������
��1���о����еĻ����¼�����д���������
��2���涨ȡ���ĺ������żǷ֣�ȡ���İ������ŵ�2���Ƿ֣�ȡ����������ļǷ�֮��Ϊһ��ȡ��ĵ÷֣���һ��ȡ��ĵ÷ֲ�С��6�ĸ��ʣ�
���𰸡�
��1���⣺һ��������װ��������ŷֱ�Ϊ1��2��3�ĺ����������ŷֱ�Ϊ1��2��3�İ���
�����������ŷֱ��Ϊa1��a2��a3�������������ŷֱ��Ϊb1��b2��b3��
���е�6�������ɫ�ͱ����û���κβ��죬�ִӴ���һ�������ȡ��������
���еĻ����¼�Ϊ��
{a1��a2}��{a1��a3}��{a1��b1}��{a1��b2}��{a1��b3}��{a2��a3}��{a2��b1}��{a2��b2}��
{a2��b3}��{a3��b1}��{a3��b2}��{a3��b3}��{b1��b2}��{b1��b3}��{b2��b3}��
����15�������¼���
��2���⣺һ��ȡ��õ������л����¼�����Ӧ�÷�Ϊ��������Ϊһ��ȡ��ĵ÷֣���
{a1��a2}��3����{a1��a3}��4����{a1��b1}��3����{a1��b2}��5����{a1��b3}��7����
{a2��a3}��5����{a2��b1}��4����{a2��b2}��6����{a2��b3}��8����{a3��b1}��5����
{a3��b2}��7����{a3��b3}��9����{b1��b2}��6����{b1��b3}��8����{b2��b3}��10����
���¼�AΪ��һ��ȡ��ĵ÷ֲ�С��6����
���¼�A�����Ļ����¼�Ϊ��
{a1��b3}��{a2��b2}��{a2��b3}��{a3��b2}��{a3��b3}��{b1��b2}��{b1��b3}��{b2��b3}��
��8����
��һ��ȡ��ĵ÷ֲ�С��6�ĸ���p= ![]()
����������1�������оٷ���������еĻ����¼�����2������֪�����оٷ������һ��ȡ��ĵ÷ֲ�С��6�ĸ��ʣ�


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��P������C1:(x-2)2+y2=4�ϵĶ���,������ԭ��OΪ����,x���������Ϊ����
����������ϵ,����P�Ƽ���O��ʱ��90�õ���Q,���Q�Ĺ켣Ϊ����C2.
������C1,C2�ļ����귽��;
����=![]() (>0)������C1,C2�ֱ���A,B����,����M(2,0),��MAB�����
(>0)������C1,C2�ֱ���A,B����,����M(2,0),��MAB�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2BC=4��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE����MΪ�߶�A1C���е㣬���ڡ�ADE��ת�����У� ��|BM|�Ƕ�ֵ��
�ڵ�M��Բ���˶���
��һ������ij��λ�ã�ʹDE��A1C��
��һ������ij��λ�ã�ʹMB��ƽ��A1DE��
������ȷ�������ǣ� ��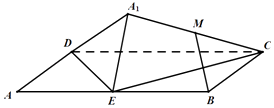
A.�٢ڢ�
B.�٢ڢ�
C.�٢ۢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���輯��A={1��2��3��4��5��6}��B={4��5��6��7��8}��������SA��S��B���ļ���S�ĸ����ǣ� ��
A.57
B.56
C.49
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() Ϊ������������У�
Ϊ������������У� ![]() ��
��![]() ��Ϊ�ȱ������Σ���ƽ��
��Ϊ�ȱ������Σ���ƽ��![]() ƽ��
ƽ��![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() .
.

��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2���������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��
�� ![]() .��1������
.��1������![]() �ļ�ֵ��ĸ�������2��������
�ļ�ֵ��ĸ�������2��������![]() ������
������![]() .��i����ʵ��
.��i����ʵ��![]() ��ȡֵ��Χ����ii����֤������
��ȡֵ��Χ����ii����֤������![]() ������ʽ
������ʽ![]() ����.
����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f��x+1���Ķ�������[��1��3]����y=f��x2���Ķ������ǣ� ��
A.[0��4]
B.[0��16]
C.[��2��2]
D.[1��4]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ԲC�� ![]() ����A,B�ֱ������Ҷ��㣬���ҽ���F��ֱ��MN������x�ᣩ������ԲC��M��N����.
����A,B�ֱ������Ҷ��㣬���ҽ���F��ֱ��MN������x�ᣩ������ԲC��M��N����.
��1������ԲC���� �������߷���Ϊ
�������߷���Ϊ![]() ������ԲC�ķ��̣�
������ԲC�ķ��̣�
��2����ֱ��BN��б����ֱ��AMб�ʵ�2��������ԲC��������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪R�ϵ��溯��f��x����ż����g��x������f��x��+g��x��=ax��a��x+2��a��0����a��1������g��2��=a����f��2����ֵΪ��
A.![]()
B.2
C.![]()
D.a2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com